- 入门教程
- 分类教程
- 回归教程
- 聚类教程
- KNN教程

回归是另一个重要且广泛使用的统计和机器学习工具。基于回归的任务的主要目标是针对给定的输入数据,预测输出标签或响应,输出将基于模型在训练阶段学到的知识。基本上,回归模型使用输入数据特征及其对应的连续数字输出值(因变量或输出变量)来学习输入与对应输出之间的特定关联。
回归类型
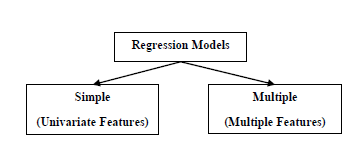
回归模型具有以下两种类型-
简单回归模型 - 这是最基本的回归模型,其中,预测是根据数据的单变量特征形成的。
多元回归模型 - 顾名思义,在该回归模型中,预测是根据数据的多个特征形成的。
代码实现
可以像构造分类器一样构造Python中的Regressor模型,Scikit-learn,一个用于机器学习的Python库,也可以用于在Python中构建一个回归器。
在以下示例中,无涯教程将构建基本的回归模型,该模型将使一条线适合数据,即线性回归器。在Python中构建回归器的必要步骤如下-
第1步 - 导入包
为了使用scikit-learn构建回归器,需要将其与其他必要的软件包一起导入。可以使用以下脚本导入-
来源:LearnFk无涯教程网
import numpy as np from sklearn import linear_model import sklearn.metrics as sm import matplotlib.pyplot as plt
第2步 - 导入数据集
导入必要的程序包后,需要一个数据集来构建回归预测模型,可以从sklearn数据集中导入它,也可以根据需要使用其他一个,将使用保存的输入数据。可以在以下脚本的帮助下导入它-
input=r'C:\linear.txt'
接下来,需要加载此数据,正在使用 np.loadtxt 函数进行加载。
input_data=np.loadtxt(input, delimiter=',') X, y=input_data[:, :-1], input_data[:, -1]
第3步 - 数据整理
由于无涯教程需要在看不见的数据上测试模型,因此,将数据集分为两部分:训练集和测试集。以下命令将执行它-
training_samples = int(0.6 * len(X)) testing_samples = len(X) - num_training X_train, y_train = X[:training_samples], y[:training_samples] X_test, y_test = X[training_samples:], y[training_samples:]
第4步 - 模型评估和预测
将数据划分为训练和测试后,需要构建模型,为此,将使用Scikit-learn的LineaRegression()函数,以下命令将创建一个线性回归对象。
reg_linear=linear_model.LinearRegression()
接下来,使用以下训练样本训练此模型:
reg_linear.fit(X_train, y_train)
现在,最后需要对测试数据进行预测。
y_test_pred=reg_linear.predict(X_test)
第5步 - 绘图和可视化
经过预测,无涯教程可以在以下脚本的帮助下进行绘制和可视化-
plt.scatter(X_test, y_test, color = 'red') plt.plot(X_test, y_test_pred, color = 'black', linewidth = 2) plt.xticks(()) plt.yticks(()) plt.show()
输出
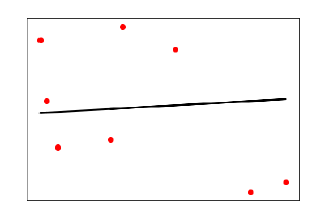
在上面的输出中,可以看到数据点之间的回归线。
第6步 - 性能计算
print("Regressor model performance:") print("Mean absolute error(MAE) =", round(sm.mean_absolute_error(y_test, y_test_pred), 2)) print("Mean squared error(MSE) =", round(sm.mean_squared_error(y_test, y_test_pred), 2)) print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2)) print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2)) print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))
输出
Regressor model performance: Mean absolute error(MAE)=1.78 Mean squared error(MSE)=3.89 Median absolute error=2.01 Explain variance score=-0.09 R2 score=-0.09
祝学习愉快!(内容编辑有误?请选中要编辑内容 -> 右键 -> 修改 -> 提交!)
 《Python机器学习入门教程》
《Python机器学习入门教程》 