关注我们

TensorFlow - 形成图

偏微分方程(PDE)是一个微分方程，它涉及具有多个独立变量的未知函数的偏导数，关于偏微分方程，无涯教程将专注于创建新图。

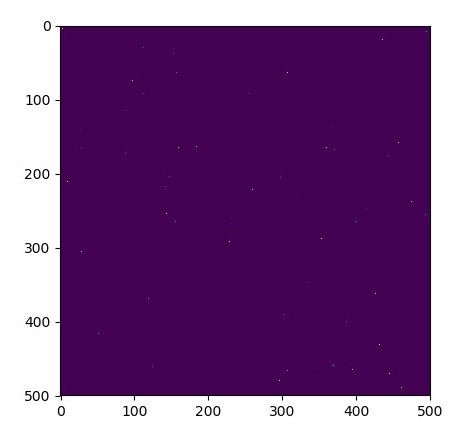
假设有一个尺寸为500 * 500平方的池塘-

N=500

现在，将计算偏微分方程并使用它形成相应的图，考虑下面给出的计算图形的步骤。

步骤1 - 导入库以进行仿真。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

步骤2 - 包括用于将2D数组转换为卷积内核和简化2D卷积运算的函数。

def make_kernel(a):
   a=np.asarray(a)
   a=a.reshape(list(a.shape) + [1,1])
   return tf.constant(a, dtype=1)

def simple_conv(x, k):
   """A simplified 2D convolution operation"""
   x=tf.expand_dims(tf.expand_dims(x, 0), -1)
   y=tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding='SAME')
   return y[0, :, :, 0]

def laplace(x):
   """Compute the 2D laplacian of an array"""
   laplace_k=make_kernel([[0.5, 1.0, 0.5], [1.0, -6., 1.0], [0.5, 1.0, 0.5]])
   return simple_conv(x, laplace_k)
   
sess=tf.InteractiveSession()

步骤3 - 包括迭代次数并计算图以相应地显示记录。

N=500

# 初始条件 - 有些雨滴击中了一个池塘

# 将所有东西设置为零
u_init=np.zeros([N, N], dtype=np.float32)
ut_init=np.zeros([N, N], dtype=np.float32)

# 一些雨滴在随机点击中了一个池塘
for n in range(100):
   a,b=np.random.randint(0, N, 2)
   u_init[a,b]=np.random.uniform()

plt.imshow(u_init)
plt.show()

# 参数：
# eps -- time resolution
# damping -- wave damping
eps=tf.placeholder(tf.float32, shape=())
damping=tf.placeholder(tf.float32, shape=())

# 为仿真状态创建变量
U=tf.Variable(u_init)
Ut=tf.Variable(ut_init)

# 离散的PDE更新规则
U_=U + eps * Ut
Ut_=Ut + eps * (laplace(U) - damping * Ut)

# 操作更新状态
step=tf.group(U.assign(U_), Ut.assign(Ut_))

# 将状态初始化为初始条件
tf.initialize_all_variables().run()

# 运行1000步PDE
for i in range(1000):
   # 步骤仿真
   step.run({eps: 0.03, damping: 0.04})
   
   # 每50个步骤可视化
   if i % 500 == 0:
      plt.imshow(U.eval())
      plt.show()