Python 微积分和微分方程详解

在本章中，我们将讨论与微积分相关的各种主题。微积分是涉及微分和积分过程的数学分支。几何上，函数的导数表示函数曲线的梯度，函数的积分表示函数曲线下的面积。当然，这些特征只在某些情况下成立，但它们为本章提供了合理的基础。

我们从一类简单函数的微积分开始：多项式。在第一个配方中，我们创建了一个表示多项式的类，并定义了区分和集成多项式的方法。多项式很方便，因为多项式的导数或积分也是多项式。然后，我们使用 Symphy 包对更一般的函数执行符号微分和积分。之后，我们将看到使用 SciPy 软件包求解方程的方法。接下来，我们将注意力转向数值积分（求积）和求解微分方程。我们使用 SciPy 软件包求解常微分方程和常微分方程组，然后使用有限差分格式求解一个简单的偏微分方程。最后，我们使用快速傅立叶变换对噪声信号进行处理并滤除噪声。

在本章中，我们将介绍以下配方：

除了科学 Python 包 NumPy 和 SciPy 之外，我们还需要 SymPy 包。可以使用您最喜欢的软件包管理器安装，例如pip：

          python3.8 -m pip install sympy

本章的代码可以在 GitHub 存储库的的Chapter 03文件夹中找到 https://github.com/PacktPublishing/Applying-Math-with-Python/tree/master/Chapter%2003 。

查看以下视频以查看代码的运行：https://bit.ly/32HuH4X 。

多项式是数学中最简单的函数之一，定义为和：

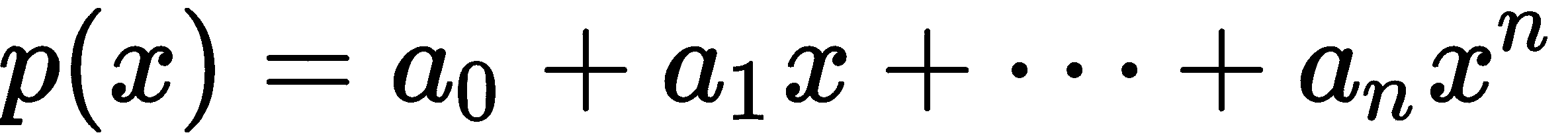
x表示要替换的占位符，a_i为数字。由于多项式很简单，它们为微积分的简要介绍提供了一个很好的方法。微积分涉及函数的微分和积分。粗略地说，积分是反微分，在这个意义上，先积分然后微分产生原始函数。

在这个配方中，我们将定义一个表示多项式的简单类，并为这个类编写执行微分和积分的方法。

准备

几何上，通过微分得到的函数的导数是其梯度，通过积分得到的函数的积分是函数曲线与【T10 x 轴之间的面积，说明曲线是位于轴的上方还是下方。在实践中，微分和积分是象征性的，使用一组规则和标准结果，这些规则和结果对于多项式来说特别简单。

此配方不需要额外的包装。

怎么做。。。

以下步骤描述如何创建一个表示多项式的类，并为该类实现微分和积分方法：

1. 让我们首先定义一个简单的类来表示多项式：

class Polynomial:
    """Basic polynomial class"""

    def __init__(self, coeffs):
        self.coeffs = coeffs

    def __repr__(self):
        return f"Polynomial({repr(self.coeffs)})"

    def __call__(self, x):
        return sum(coeff*x**i for i, coeff 
                in enumerate(self.coeffs))

2. 现在我们已经为多项式定义了一个基本类，我们可以继续为这个Polynomial类实现微分和积分运算，以说明这些运算如何改变多项式。我们从分化开始。我们通过将当前系数列表中的每个元素相乘来生成新系数，而不使用第一个元素。我们使用这个新的系数列表创建一个新的返回的Polynomial实例：

    def differentiate(self):
        """Differentiate the polynomial and return the derivative"""
        coeffs = [i*c for i, c in enumerate(self.coeffs[1:], start=1)]
        return Polynomial(coeffs)

3. 为了实现积分方法，我们需要创建一个新的系数列表，其中包含参数给定的新常量（转换为浮点以保持一致性）。然后，我们将旧系数除以其在列表中的新位置添加到该系数列表中：

    def integrate(self, constant=0):
        """Integrate the polynomial, returning the integral"""
        coeffs = [float(constant)] 
        coeffs += [c/i for i, c in enumerate(self.coeffs, start=1)]
        return Polynomial(coeffs)

4. 最后，为了确保这些方法按预期工作，我们应该用一个简单的案例来测试这两种方法。我们可以使用一个非常简单的多项式来检查这一点，例如x²-2x+1：

p = Polynomial([1, -2, 1])
p.differentiate()
# Polynomial([-2, 2])
p.integrate(constant=1)
# Polynomial([1.0, 1.0, -1.0, 0.3333333333])

它是如何工作的。。。

多项式为微积分的基本运算提供了一个简单的介绍，但是为其他一般函数类构造 Python 类并不那么容易。也就是说，多项式是非常有用的，因为它们很容易理解，也许更重要的是，多项式的微积分非常容易。对于变量x的幂，微分规则是乘以幂并将幂减 1，使xⁿ变为nx^n-1。

积分更复杂，因为函数的积分不是唯一的。我们可以把任何常数加到积分上，得到第二个积分。对于一个变量x的幂，积分的规则是将幂增加 1，然后除以新的幂，这样xⁿ变成xⁿ⁺¹/（n+1，为了积分一个多项式，我们增加x的每一个幂除以 1，并将相应的系数除以新的幂。

我们在菜谱中定义的Polynomial类相当简单，但它代表了核心思想。多项式由其系数唯一确定，我们可以将其存储为数值列表。微分和积分是我们可以在这个系数列表上执行的操作。我们包括一个简单的__repr__方法来帮助显示Polynomial对象，以及一个__call__方法来帮助评估特定数值。这主要是为了演示多项式的求值方式。

多项式对于解决某些涉及计算昂贵函数的问题非常有用。对于此类问题，我们有时可以使用某种多项式插值，将一个多项式“拟合”到另一个函数，然后利用多项式的性质帮助解决原始问题。计算多项式要比原始函数“便宜”得多，因此这可以大大提高速度。这通常是以牺牲一些准确性为代价的。例如，Simpson 近似曲线下面积的规则通过三个连续网格点定义的间隔上的二次多项式来近似曲线。通过积分可以很容易地计算出每个二次多项式下面的面积。

还有更多。。。

多项式在计算编程中的作用比简单地证明微分和积分的效果要重要得多。因此，NumPy 包numpy.polynomial中提供了更丰富的Polynomial类。NumPyPolynomial类和各种派生子类在各种数值问题中都很有用，并且支持算术运算和其他方法。特别是，有一些方法可以将多项式拟合到数据集合中。

NumPy 还提供了派生自Polynomial的类，这些类表示各种特殊类型的多项式。例如，Legendre类表示一个称为勒让德多项式的特定多项式系统。勒让德多项式是为满足-1 的x定义的≤ x≤ 1并形成一个正交系统，这对于数值积分和有限元法求解偏微分方程等应用非常重要。勒让德多项式是使用递归关系定义的。我们定义

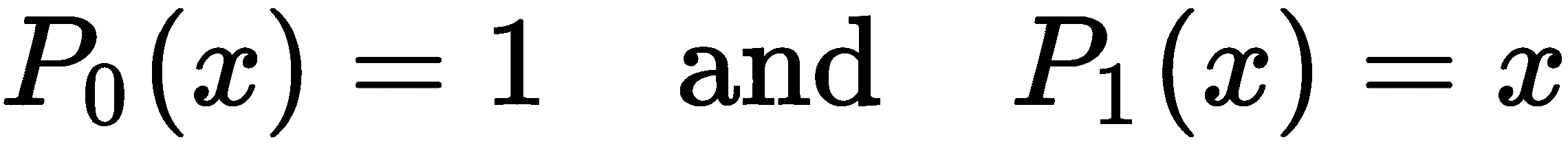
每n≥ 2定义了满足递推关系的n次勒让德多项式，

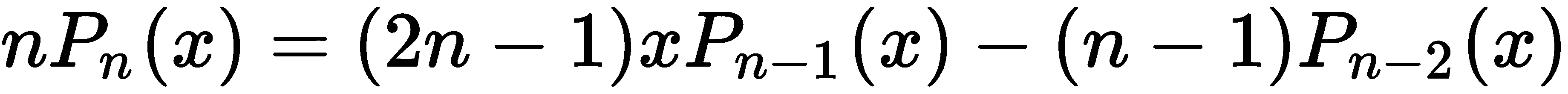
还有其他几个所谓的正交（系统）多项式，包括*拉盖尔*多项式、切比雪夫多项式和埃尔米特多项式。

另见

微积分当然在数学教科书中有很好的记载，而且有许多教科书涵盖了从基本方法到深层理论的所有内容。正交多项式系统在数值分析文本中也有很好的记录。

在某些情况下，您可能需要区分一个不是简单多项式的函数，并且您可能需要以某种自动方式进行区分，例如，如果您正在编写教育软件。Python 科学堆栈包括一个名为 Symphy 的包，它允许我们在 Python 中创建和操作符号数学表达式。特别是，Symphy 可以执行符号函数的微分和积分，就像数学家一样。

在本配方中，我们将创建一个符号函数，然后使用 Symphy 库对该函数进行区分和集成。

准备

与其他一些 scientific Python 包不同，文献中似乎没有标准的别名来导入 Symphy。相反，文档在多个点上使用星型导入，这与 PEP8 样式指南不一致。这可能是为了使数学表达式更自然。我们将简单地以其名称sympy导入模块，以避免与scipy包的标准缩写sp（这也是sympy的自然选择）混淆：

import sympy

在此配方中，我们将定义一个表示函数的符号表达式

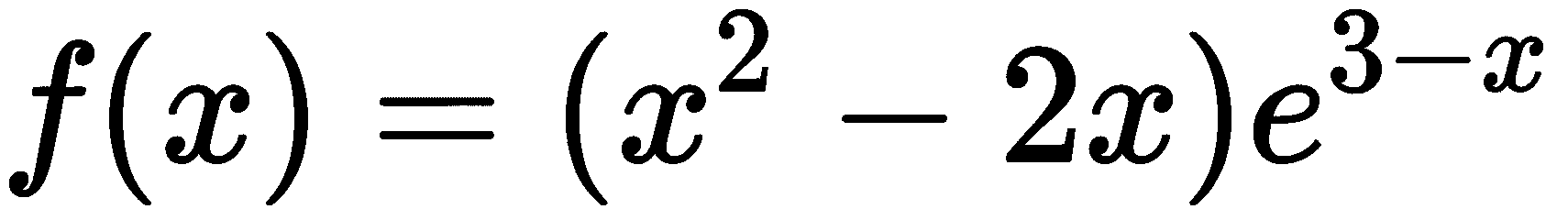
怎么做。。。

使用 Symphy 软件包可以很容易地进行象征性的区分和集成（就像您手工操作一样）。按照以下步骤查看如何完成此操作：

1. 导入 SymPy 后，我们定义将出现在表达式中的符号。这是一个 Python 对象，与数学变量一样，它没有特定的值，但可以在公式和表达式中同时表示许多不同的值。对于这个配方，我们只需要为x定义一个符号，因为除此之外，我们只需要常量（文字）符号和函数。我们使用sympy中的symbols例程定义一个新符号。为了保持符号简单，我们将此新符号命名为x：

x = sympy.symbols('x')

2. 使用symbols函数定义的符号支持所有算术运算，因此我们可以直接使用刚才定义的符号x构造表达式：

f = (x**2 - 2*x)*sympy.exp(3 - x)

3. 现在我们可以使用 Symphy 的符号演算功能来计算f的导数，即微分f。我们使用sympy中的diff例程来实现这一点，该例程将符号表达式与指定符号区分开来，并返回导数表达式。这通常不是以最简单的形式表示的，因此我们使用sympy.simplify例程来简化结果：

fp = sympy.simplify(sympy.diff(f))  # (x*(2 - x) + 2*x - 2)
                                                       *exp(3 - x)

4. 与手工计算的导数（定义为 Symphy 表达式）相比，我们可以检查使用 Symphy 的符号微分的结果是否正确，如下所示：

fp2 = (2*x - 2)*sympy.exp(3 - x) - (x**2 - 2*x)*sympy.exp(3 - x)

5. SymPy equality 测试两个表达式是否相等，但不测试它们在符号上是否相等。因此，我们必须首先将我们希望测试的两个语句的差异简化为0：

sympy.simplify(fp2 - fp) == 0  # True

6. 我们可以使用 SymPy 和integrate函数来集成函数f。通过提供符号作为第二个可选参数，还可以提供用于执行集成的符号：

F = sympy.integrate(f, x)  # -x**2*exp(3 - x)

它是如何工作的。。。

SymPy 定义了各种类来表示某些类型的表达式。例如，由Symbol类表示的符号是原子表达式的示例。表达式的构建方式与 Python 从源代码构建抽象语法树的方式类似。然后可以使用方法和标准算术运算操纵这些表达式对象。

Symphy 还定义了标准的数学函数，可以对Symbol对象进行操作，以创建符号表达式。最重要的特征是能够执行符号演算——而不是我们在本章剩余部分探讨的数值演算——并给出精确（有时称为解析的演算问题解决方案。

Symphy 包中的diff例程对这些符号表达式执行微分。这个例程的结果通常不是最简单的形式，这就是为什么我们使用simplify例程来简化配方中的导数。integrate例程象征性地集成了与给定符号相关的scipy表达式。（diff例程还接受一个符号参数，该参数指定要区分的符号。）这将返回一个表达式，其导数是原始表达式。此例程不添加积分常数，这是手工进行积分的良好实践。

还有更多。。。

SymPy 可以做的远不止简单的代数和微积分。数学的各个领域都有子模块，如数论、几何和其他离散数学（如组合数学）。

SymPy 表达式（和函数）可以内置到 Python 函数中，这些函数可以应用于 NumPy 数组。这是使用来自sympy.utilities模块的lambdify例程完成的。这会将 SymPy 表达式转换为数值表达式，该表达式使用 SymPy 标准函数的 NumPy 等效项对表达式进行数值计算。结果类似于定义 Python Lambda，因此得名。例如，我们可以使用以下例程将此配方中的函数和派生函数转换为 Python 函数：

from sympy.utilities import lambdify
lam_f = lambdify(x, f)
lam_fp = lambdify(x, fp)

lambdify例程接受两个参数。第一个是要提供的变量，x在前面的代码块中，第二个是调用此函数时要计算的表达式。例如，我们可以将前面定义的 lambdified SymPy 表达式作为普通 Python 函数进行计算：

lam_f(4)  # 2.9430355293715387
lam_fp(7)  # -0.4212596944408861

我们甚至可以在 NumPy 数组上计算这些 lambdified 表达式：

lam_f(np.array([0, 1, 2]))  # array([ 0\. , -7.3890561, 0\. ])

The lambdify routine uses the Python exec routine to execute the code, so it should not be used with unsanitized input.

许多数学问题最终归结为求解形式为f（x）=0 的方程，其中f是单个变量的函数。在这里，我们试图找到一个方程成立的值x。方程适用的x的值有时称为方程的根。有许多算法可用于求解这种形式的方程。在本配方中，我们将使用牛顿-拉斐逊法和割线法求解形式为f（x）=0 的方程。

牛顿-拉斐逊法（Newton's method）和割线法是很好的标准寻根算法，几乎可以应用于任何情况。这些是迭代方法，从根的近似开始，迭代改进此近似，直到它位于给定公差范围内。

为了演示这些技术，我们将使用符号演算中的函数，使用由

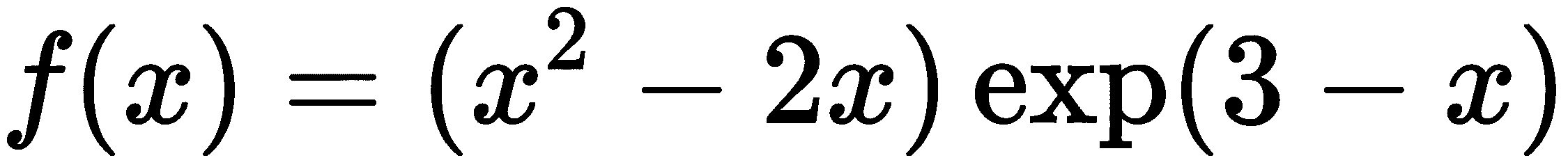
它是为x的所有实值定义的，正好有两个根，一个在x处=0，一个在x处=2。

准备

SciPy 包包含求解方程的例程（以及许多其他内容）。根查找例程可以在scipy包的optimize模块中找到。

如果您的方程式的格式不是f（x）=0，那么您需要重新排列它，使其成为实际情况。这通常不太困难，只需要将右侧的任何术语移到左侧即可。例如，如果您希望找到一个函数的不动点，即当g（x）=x时，我们会将该方法应用于f（x=g（【T18 x-x】给出的相关函数。

怎么做。。。

optimize包提供了数值根查找的例程。以下说明描述了如何使用本模块中的newton例程：

1. optimize模块未列在scipy名称空间中，因此必须单独导入：

from scipy import optimize

2. 然后我们必须用 Python 定义此函数及其派生函数：

from math import exp

def f(x):
    return x*(x - 2)*exp(3 - x)

3. 该函数的导数在上一个配方中计算：

def fp(x):
    return -(x**2 - 4*x + 2)*exp(3 - x)

4. 对于 Newton-Raphson 方法和割线方法，我们使用来自optimize的newton例程。割线法和牛顿-拉斐逊法都要求函数和第一个参数以及第一个近似值x0作为第二个参数。要使用 Newton-Raphson 方法，我们必须使用fprime关键字参数提供f的导数：

optimize.newton(f, 1, fprime=fp) # Using the Newton-Raphson method
# 2.0

5. 要使用割线方法，只需要函数，但必须提供根的前两个近似值；第二个作为x1关键字参数提供：

optimize.newton(f, 1., x1=1.5) # Using x1 = 1.5 and the secant method
# 1.9999999999999862

Neither the Newton-Raphson nor the secant method are guaranteed to converge to a root. It is perfectly possible that the iterates of the method will simply cycle through a number of points (periodicity) or fluctuate wildly (chaos).

它是如何工作的。。。

利用该公式迭代定义了函数*fx、导数f’x和初始近似x₀*的牛顿-拉斐逊法

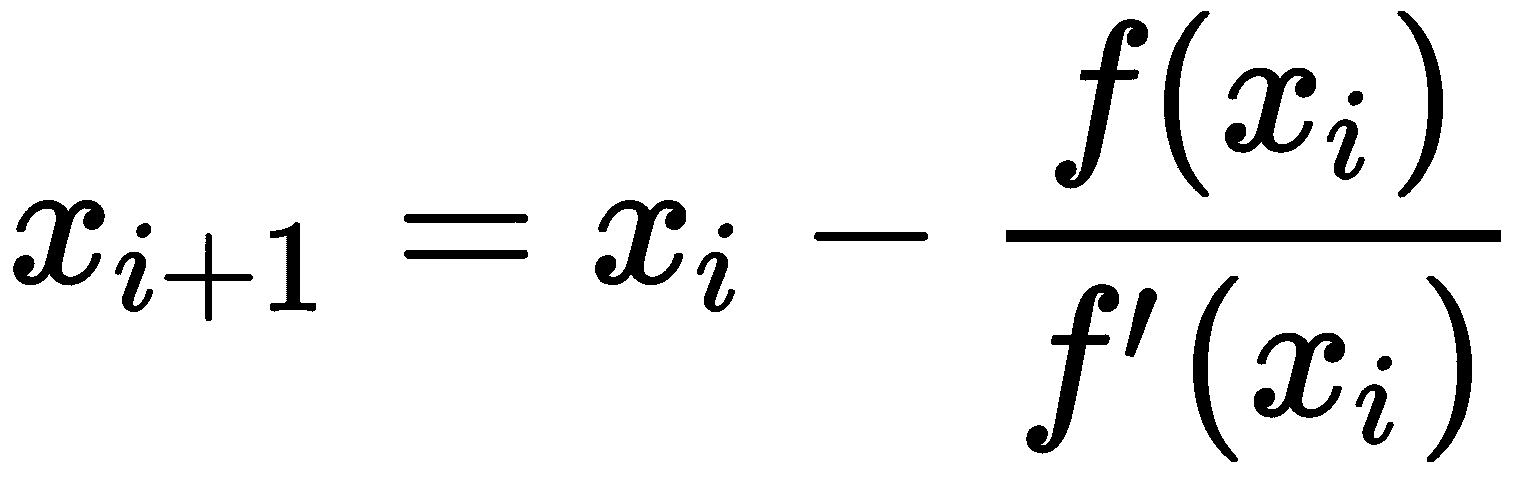
对于每个整数i≥ 0。从几何角度来看，如果*f（x_i0或fx_i*为正（因此函数增加），则考虑梯度为负的方向（因此函数减小）o。

割线法基于牛顿-拉斐逊法，但用近似代替了一阶导数

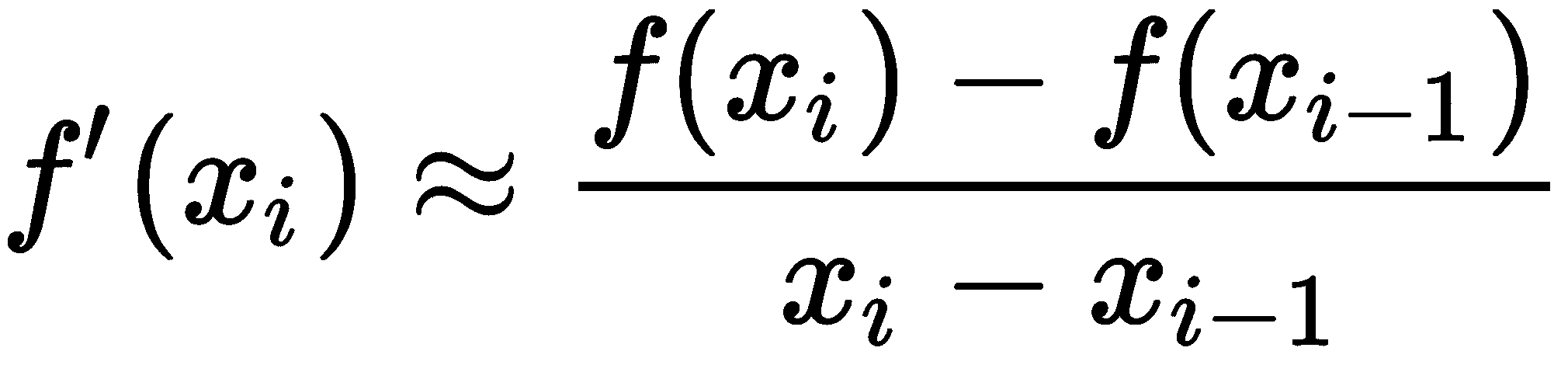
当x_i-x_i-1足够小时，如果方法收敛，就会出现这种情况，那么这是一个很好的近似值。不需要函数f的导数所付出的代价是，我们需要额外的初始猜测来启动该方法。该方法的公式如下所示：

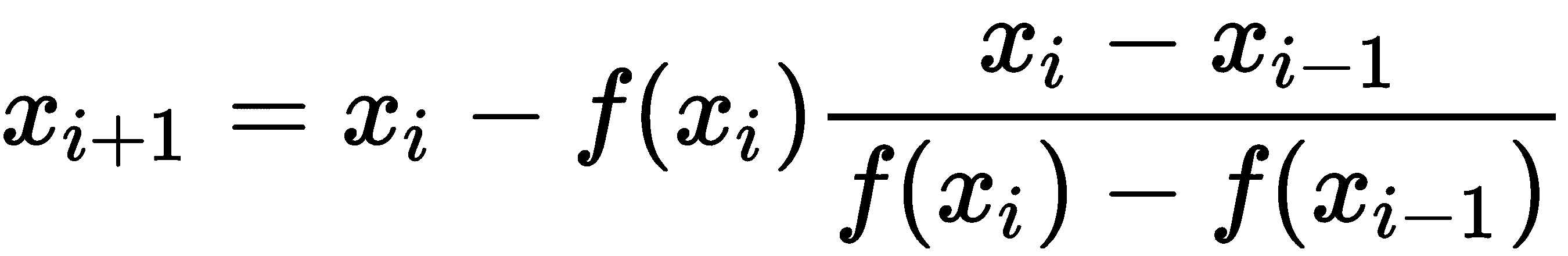
一般来说，如果给任一方法一个足够接近根的初始猜测（割线法的猜测），则该方法将收敛到该根。如果在一次迭代中导数为零，牛顿-拉斐逊方法也可能失败，在这种情况下，公式没有很好地定义。

还有更多。。。

本配方中提到的方法是通用方法，但在某些情况下，还有其他方法可能更快或更准确。广义地说，寻根算法分为两类：在每次迭代中使用函数梯度信息的算法（牛顿-拉斐逊、割线、哈雷）和要求根位置有界的算法（对分法、regula-falsi、Brent）。到目前为止讨论的算法属于第一类，虽然通常相当快，但可能无法收敛。

第二类算法是已知根在指定间隔a 内存在的算法≤ x≤ b。我们可以通过检查f（a）和f（b）是否有不同的符号，即f（a<0fb中的一个，来检查根是否位于这样的间隔内或*f*b<0<fa为真。（当然，前提是函数是连续的，在实践中往往是如此。）这种最基本的算法是对分算法，它反复对分区间，直到找到足够好的根近似值。基本前提是在中点拆分a和b之间的间隔，并选择功能改变符号的间隔。该算法重复执行，直到间隔非常小。以下是该算法在 Python 中的基本实现：

from math import copysign

def bisect(f, a, b, tol=1e-5):
    """Bisection method for root finding"""
    fa, fb = f(a), f(b)
    assert not copysign(fa, fb) == fa, "Function must change signs"
    while (b - a) > tol:
        m = (b - a)/2 # mid point of the interval
        fm = f(m)
        if fm == 0:
            return m
        if copysign(fm, fa) == fm: # fa and fm have the same sign
            a = m
            fa = fm
        else: # fb and fm have the same sign
            b = m
        return a

该方法保证收敛，因为在每一步距离b-a都减半。然而，该方法可能需要比牛顿-拉斐逊法或割线法更多的迭代次数。对分法的一个版本也可以在optimize中找到。这个版本是用 C 语言实现的，比这里介绍的版本效率更高，但是在大多数情况下，二分法并不是最快的方法。

Brent 的方法是对分法的改进，在optimize模块中作为brentq提供。它使用二等分和插值的组合来快速找到方程的根：

optimize.brentq(f, 1.0, 3.0)  # 1.9999999999998792

需要注意的是，涉及括号的技术（二分法、regula-falsi、Brent）不能用于求复变量的根函数，而不使用括号的技术（牛顿、割线、哈雷）可以。

积分可以解释为位于曲线和x轴之间的区域，根据该区域位于轴的上方还是下方进行标记。有些积分不能用符号方法直接计算，而必须用数值近似。一个典型的例子是高斯误差函数，在第一章、基本包、函数和概念中的基本数学函数一节中提到了高斯误差函数。这是由公式定义的

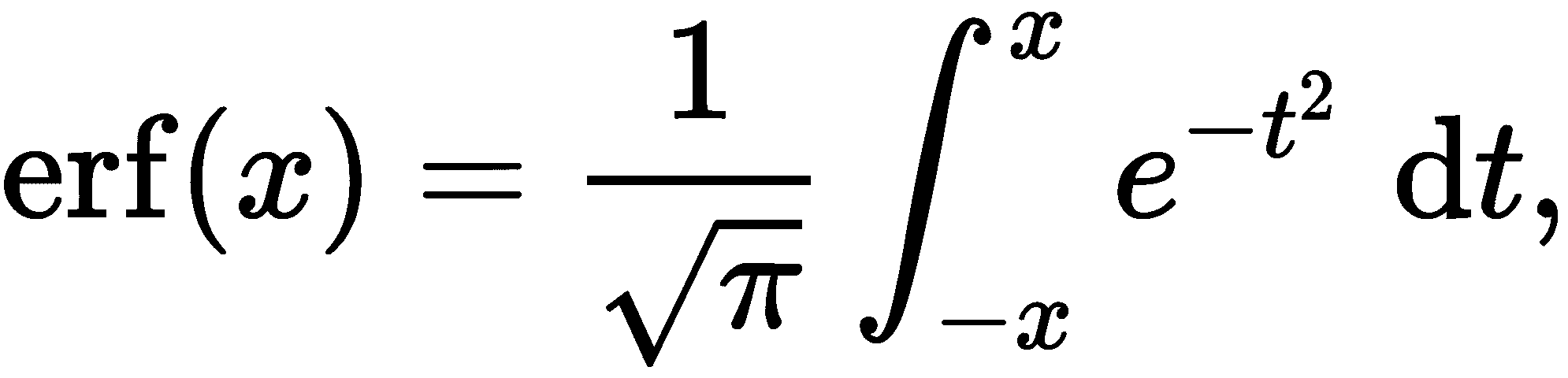
这里出现的积分不能用符号来计算。

在这个配方中，我们将看到如何使用 SciPy 包中的数值积分例程来计算函数的积分。

准备

我们使用scipy.integrate模块，该模块包含几个用于计算数值积分的例程。我们按如下方式导入此模块：

from scipy import integrate

怎么做。。。

以下步骤描述了如何使用 SciPy 对函数进行数值积分：

1. 我们在数值x=1处计算误差函数定义中出现的积分。为此，我们需要在 Python 中定义被积函数（出现在整数中的函数）：

def erf_integrand(t):
    return np.exp(-t**2)

scipy.integrate中有两个主要例程用于执行可使用的数值积分（求积）。第一个是quad功能，使用 QUADPACK 进行集成，第二个是quadrature。

2. quad例程是一个通用的集成工具。它需要三个参数，即要集成的函数（erf_integrand）、下限（-1.0）和上限（1.0：

val_quad, err_quad = integrate.quad(erf_integrand, -1.0, 1.0)
# (1.493648265624854, 1.6582826951881447e-14)

第一个返回值是整数的值，第二个是误差的估计值。

3. 使用quadrature例程重复计算，我们得到以下结果。参数与quad例程的参数相同：

val_quadr, err_quadr = integrate.quadrature(erf_integrand, -1.0,
    1.0)
# (1.4936482656450039, 7.459897144457273e-10)

输出与代码的格式相同，带有积分值，然后是误差估计值。请注意，quadrature例程的错误更大。这是当估计误差低于给定公差时方法终止的结果，该公差可在调用例程时修改。

它是如何工作的。。。

大多数数值积分技术遵循相同的基本过程。首先，我们为积分区域中的i=1，2，…，n选择点x_i，然后使用这些值和数值f（x_i来近似积分。例如，使用梯形法则，我们通过

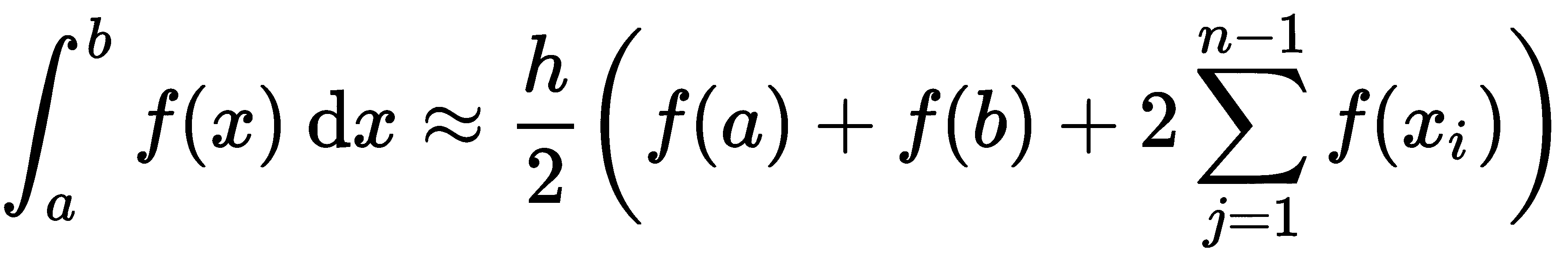
其中a<x₁<x₂<<x_n-1<b和h是相邻x_iT13】值之间的（共同）差异，包括端点a和b。这可以在 Python 中实现，如下所示：

def trapezium(func, a, b, n_steps):
    """Estimate an integral using the trapezium rule"""
    h = (b - a) / n_steps
    x_vals = np.arange(a + h, b, h) 
    y_vals = func(x_vals)
    return 0.5*h*(func(a) + func(b) + 2.*np.sum(y_vals))

quad和quadrature使用的算法远比这复杂。使用此函数来近似使用trapezium的erf_integrand积分，结果为 1.4936463036001209，这与quad和quadrature例程到小数点后 5 位的近似值一致。

quadrature例程使用固定容差高斯求积，而quad例程使用 Fortran 库 QUADPACK 例程中实现的自适应算法。对两个例程进行计时，我们发现对于配方中描述的问题，quad例程的速度大约是quadrature例程的 5 倍。quad例程的执行时间约为 27µs，平均执行时间超过 100 万次，而quadrature例程的执行时间约为 134µs。（根据您的系统，结果可能会有所不同。）

还有更多。。。

本节中提到的例程要求知道被积函数，但情况并非总是如此。相反，我们可能知道有很多对（xy）和y=f（x），但我们不知道在其他点评估的函数f。在这种情况下，我们可以使用scipy.integrate中的一种采样正交技术。如果已知点的数量非常大，并且所有点的间距相等，我们可以使用 Romberg 积分来很好地逼近积分。为此，我们使用romb例程。否则，我们可以使用梯形规则的变体（如上所述）使用trapz例程，或者使用simps例程使用辛普森规则。

微分方程出现在一个量通常随时间根据给定关系演化的情况下。它们在工程学和物理学中极为常见，并且非常自然地出现。一个（非常简单的）微分方程的经典例子是牛顿设计的冷却定律。物体的温度以与当前温度成比例的速率冷却。从数学上讲，这意味着我们可以使用微分方程写出身体在时间T>0的温度T的导数

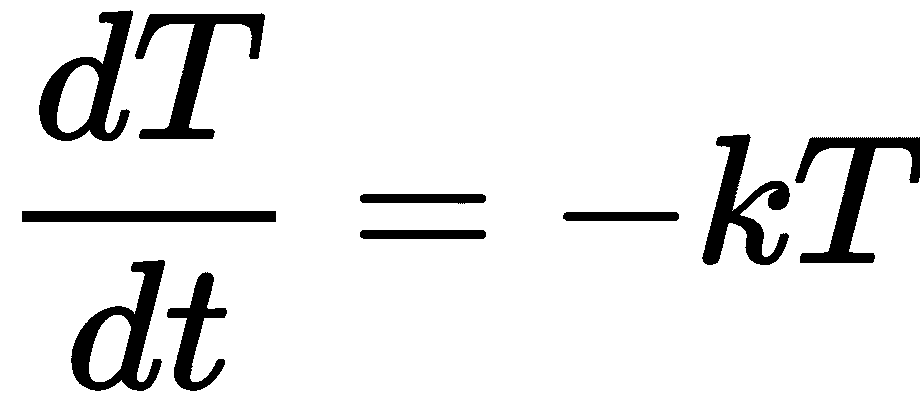
其中k是确定冷却速率的正常数。这个微分方程可以通过先“分离变量”，然后积分和重新排列来解析地求解。执行此步骤后，我们得到通解

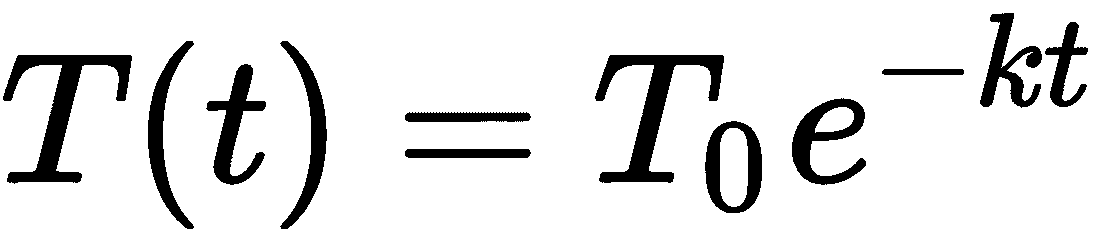
其中T₀为初始温度。

在此配方中，我们将使用 SciPy 的solve_ivp例程数值求解一个简单的常微分方程。

准备

我们将使用前面描述的冷却方程在 Python 中演示数值求解微分方程的技术，因为在这种情况下，我们可以计算真实解。我们取初始温度为T₀=50和k=0.2。让我们也为 0 到 5 之间的t值找到解决方案。

一般（一阶）微分方程的形式为

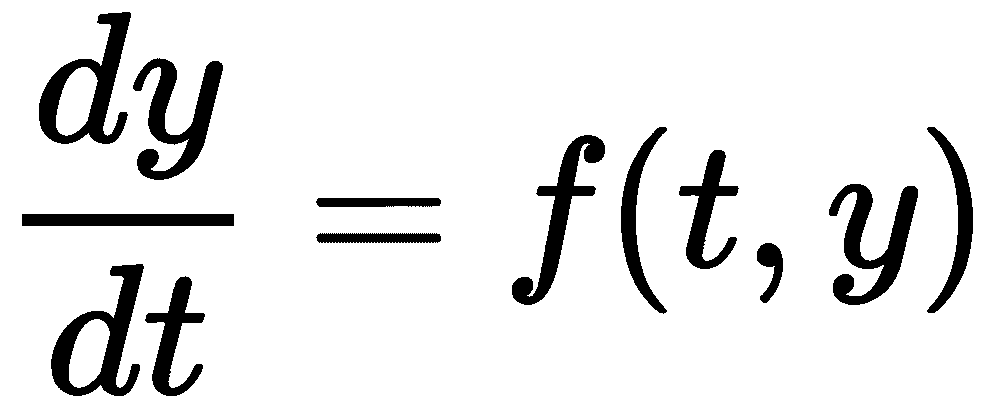
其中f是t（自变量）和y（因变量）的函数。本式中，T为因变量，f（T，T）=-kt。SciPy 包中求解微分方程的例程需要函数f和初始值y_{0以及我们需要计算解的t值的范围。首先，我们需要在 Python 中定义我们的函数f，并创建变量y0和t范围，准备提供给 SciPy 例程：}

def f(t, y):
    return -0.2*y

t_range = (0, 5)

接下来，我们需要定义应该从中找到解决方案的初始条件。出于技术原因，初始y值必须指定为一维 NumPy 数组：

T0 = np.array([50.])

因为在本例中，我们已经知道了真正的解决方案，所以我们也可以在 Python 中定义它，以便与我们将要计算的数值解决方案进行比较：

def true_solution(t):
    return 50.*np.exp(-0.2*t)

怎么做。。。

按照以下步骤数值求解微分方程，并绘制解和误差图：

1. 我们使用 SciPy 中integrate模块的solve_ivp例程数值求解微分方程。我们为最大步长添加了一个参数，其值为0.1，因此在合理数量的点上计算解：

sol = integrate.solve_ivp(f, t_range, T0, max_step=0.1)

2. 接下来，我们从solve_ivp方法返回的sol对象中提取解的值：

t_vals = sol.t
T_vals = sol.y[0, :]

3. 接下来，我们在一组轴上绘制解决方案，如下所示。由于我们还将在同一图形上绘制近似误差，因此我们使用subplots例程创建两个子图：

fig, (ax1, ax2) = plt.subplots(1, 2, tight_layout=True)
ax1.plot(t_vals, T_vals)
ax1.set_xlabel("$t$")
ax1.set_ylabel("$T$")
ax1.set_title("Solution of the cooling equation")

这将在图 3.1左侧显示的一组轴上绘制解决方案。

4. 为此，我们需要计算从solve_ivp例程获得的点的真解，然后计算真解和近似解之间差值的绝对值：

err = np.abs(T_vals - true_solution(t_vals))

5. 最后，在图 3.1的右侧，我们在y轴上用对数标度绘制近似误差。然后，我们可以使用第 2 章使用 Matplotlib的数学绘图中所示的semilogy绘图命令，使用对数刻度y轴在右侧绘制该图：

ax2.semilogy(t_vals, err)
ax2.set_xlabel("$t$")
ax2.set_ylabel("Error")
ax2.set_title("Error in approximation")

图 3.1中的左图显示温度随时间降低，而右图显示，当我们远离初始条件给出的已知值时，误差增加：

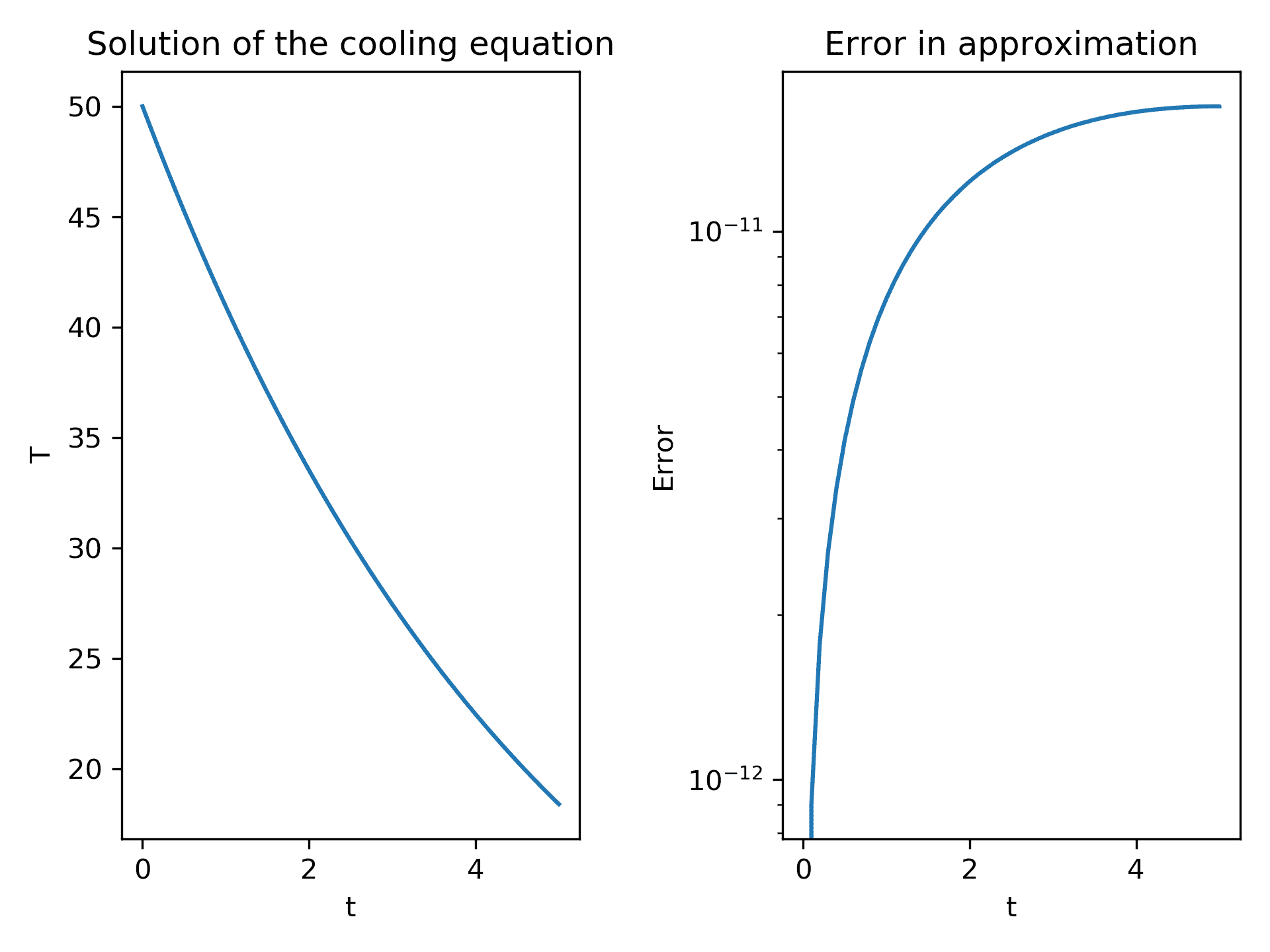
Figure 3.1: Plot of the numerical solution to the cooling equation obtained using the solve_ivp routine with default settings

它是如何工作的。。。

大多数求解微分方程的方法都是“时间步进”法。成对（t_i、y_i通过采取小t步数并近似函数y 的值来生成。最基本的时间步进法——欧拉法或许最能说明这一点。固定小步长h>0，我们使用以下公式在i步形成近似值

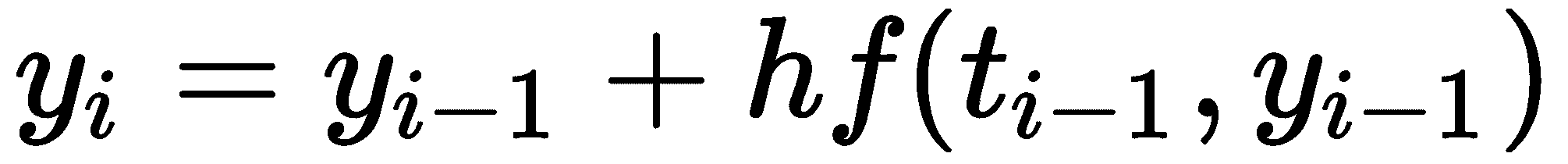
从已知初始值y₀开始。我们可以很容易地编写一个 Python 例程来执行 Euler 的方法，如下所示（当然，有许多不同的方法来实现 Euler 的方法；这是一个非常简单的示例）：

1. 首先，我们通过创建列表来设置该方法，该列表将存储我们将返回的t值和y值：

def euler(func, t_range, y0, step_size):
    """Solve a differential equation using Euler's method"""
    t = [t_range[0]]
    y = [y0]
    i = 0

2. 欧拉的方法一直持续到我们到达t范围的终点。在这里，我们使用一个while循环来实现这一点。循环体非常简单；我们首先递增一个计数器i，然后将新的t和y值附加到各自的列表中：

    while t[i] < t_range[1]:
        i += 1
        t.append(t[i-1] + step_size)  # step t
        y.append(y[i-1] + step_size*func(t[i-1], y[i-1]))  # step y
    return t, y

默认情况下，solve_ivp例程使用的方法是 Runge-Kutta-Fehlberg 方法（RK45），该方法能够调整步长，以确保近似误差保持在给定公差范围内。此例程需要三个位置参数：函数f、应该在其上找到解的t范围，以及初始y值（t₀）。可以提供可选参数来更改解算器、要计算的点数以及其他一些设置。

传递给solve_ivp例程的函数必须有两个参数，如准备一节中所述的一般微分方程。函数可以有额外的参数，可以使用solve_ivp例程的args关键字提供，但这些参数必须放在两个必要的参数之后。将我们之前定义的euler例程与solve_ivp例程（两者的步长均为 0.1）进行比较，我们发现solve_ivp解决方案之间的最大真实误差为 10^-6，而euler解决方案仅管理 31 的误差。euler例程正在工作，但步长太大，无法克服累积误差。

solve_ivp例程返回一个 solution 对象，该对象存储有关已计算的解决方案的信息。这里最重要的是t和y属性，它们包含t值，解y是根据这些值计算的，解y本身也是如此。我们使用这些值来绘制我们计算的解决方案。y值存储在(n, N)形状的 NumPy 数组中，其中n是方程的分量数（此处为 1），N是计算的点数。sol中保存的y值存储在二维数组中，在本例中，该数组有 1 行多列。我们使用切片y[0, :]提取第一行作为一维数组，可用于绘制步骤 4中的解决方案。

我们使用对数标度的y轴来绘制误差，因为有趣的是数量级。在非标度的y轴上绘制它会得到一条非常接近x轴的线，这不会显示我们通过t值时误差的增加。对数标度的y轴清楚地显示了这种增加。

还有更多。。。

solve_ivp例程是许多微分方程解算器的便捷接口，默认为 Runge-Kutta-Fehlberg（RK45）方法。不同的解算器具有不同的强度，但 RK45 方法是一种很好的通用解算器。

另见

有关如何在 Matplotlib 中向图形添加子批次的详细说明，请参见第 2 章中的添加子批次配方、使用 Matplotlib 进行数学绘图。

微分方程有时出现在由两个或多个相互关联的微分方程组成的系统中。一个经典的例子是竞争物种种群的简单模型。这是一个简单的竞争物种模型，标记为P（猎物）和W（捕食者），由以下方程式给出：

*

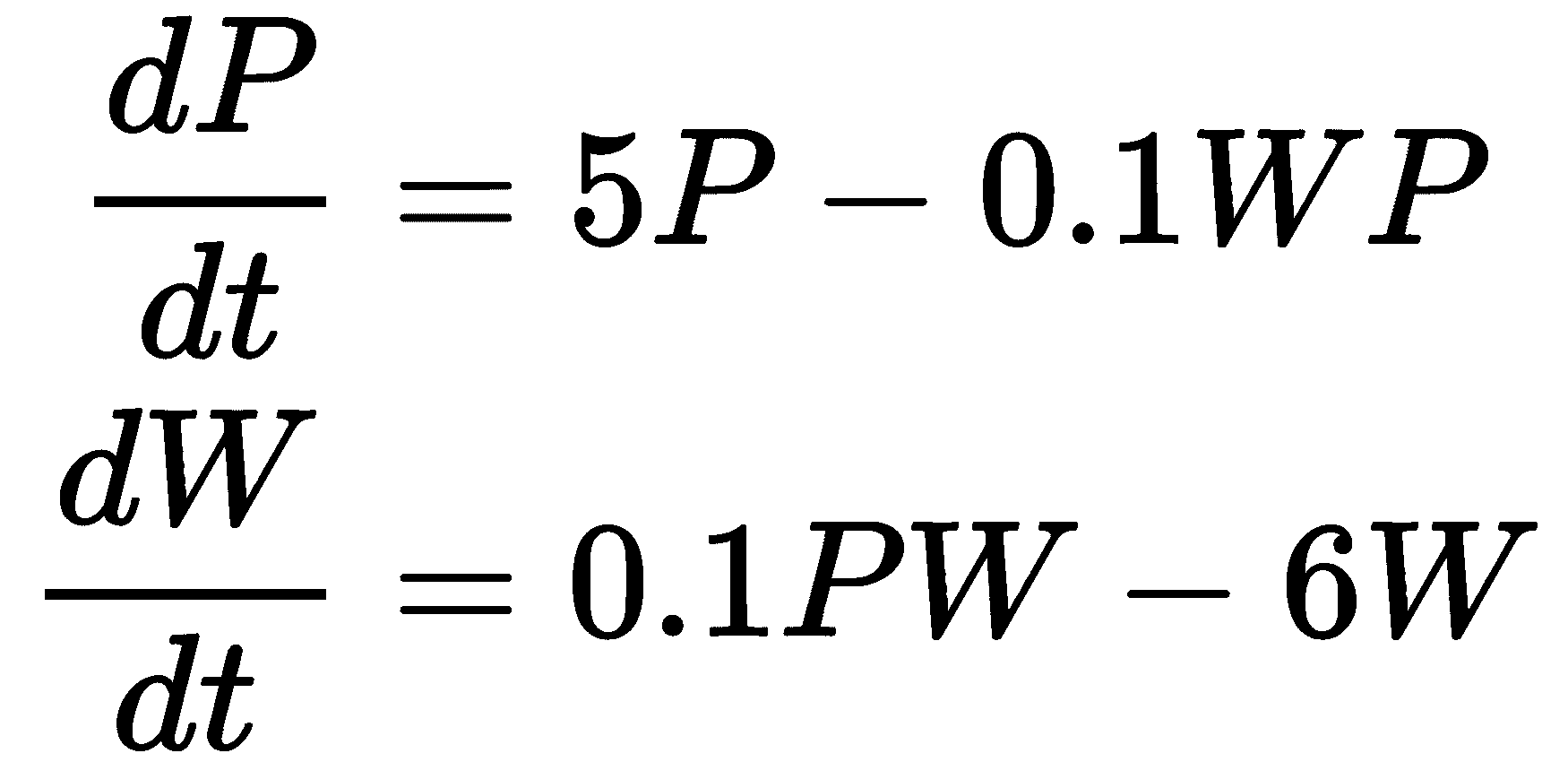
第一个方程决定了被捕食物种P的增长，如果没有任何捕食者，这将是指数增长。第二个方程决定了捕食者物种W的生长，如果没有任何猎物，它们将呈指数衰减。当然，这两个方程是耦合的；每个种群的变化都取决于两个种群。捕食者以与其两个种群的乘积成正比的速度消耗猎物，捕食者以与猎物的相对丰度成正比的速度增长（同样是两个种群的乘积）。

在本配方中，我们将分析一个简单的微分方程组，并使用 SciPyintegrate模块获得近似解。

准备

使用 Python 求解微分方程组的工具与求解单个方程的工具相同。我们再次使用 SciPy 中integrate模块的solve_ivp例程。然而，这只会给我们一个给定起始种群的预测进化。因此，我们还将使用 Matplotlib 中的一些绘图工具来更好地了解演变。

怎么做。。。

以下步骤将介绍如何分析一个简单的微分方程组：

1. 我们的第一个任务是定义一个包含方程组的函数。对于单个方程，该函数需要采用两个参数，但因变量y（在数值求解简单微分方程配方的符号中）现在将是一个包含与方程数量相同的元素的数组。这里有两个要素。本配方中示例系统所需的功能如下：

def predator_prey_system(t, y):
    return np.array([5*y[0] - 0.1*y[0]*y[1], 0.1*y[1]*y[0] -
       6*y[1]])

2. 现在我们已经用 Python 定义了这个系统，我们可以使用 Matplotlib 中的quiver例程生成一个图，该图将描述在众多初始种群中，由方程给出的种群将如何演化。我们首先建立一个点的网格，我们将在上面绘制这一演变。为quiver例程选择相对较少的点是个好主意，否则很难在绘图中看到细节。对于本例，我们绘制了介于 0 和 100 之间的总体值：

p = np.linspace(0, 100, 25)
w = np.linspace(0, 100, 25)
P, W = np.meshgrid(p, w)

3. 现在，我们计算每一对的系统值。请注意，系统中的两个方程都不是时间相关的（它们是自治的）；时间变量t在计算中并不重要。我们为t参数提供值0：

dp, dw = predator_prey_system(0, np.array([P, W]))

4. 变量dp和dw现在保持着P和W的种群将分别进化的“方向”，如果我们从网格中的每个点开始。我们可以使用matplotlib.pyplot中的quiver例程将这些方向标绘在一起：

fig, ax = plt.subplots()
ax.quiver(P, W, dp, dw)
ax.set_title("Population dynamics for two competing species")
ax.set_xlabel("P")
ax.set_ylabel("W")

绘制这些命令的结果，现在我们可以看到图 3.2，图中给出了解决方案演变的“全局”图：

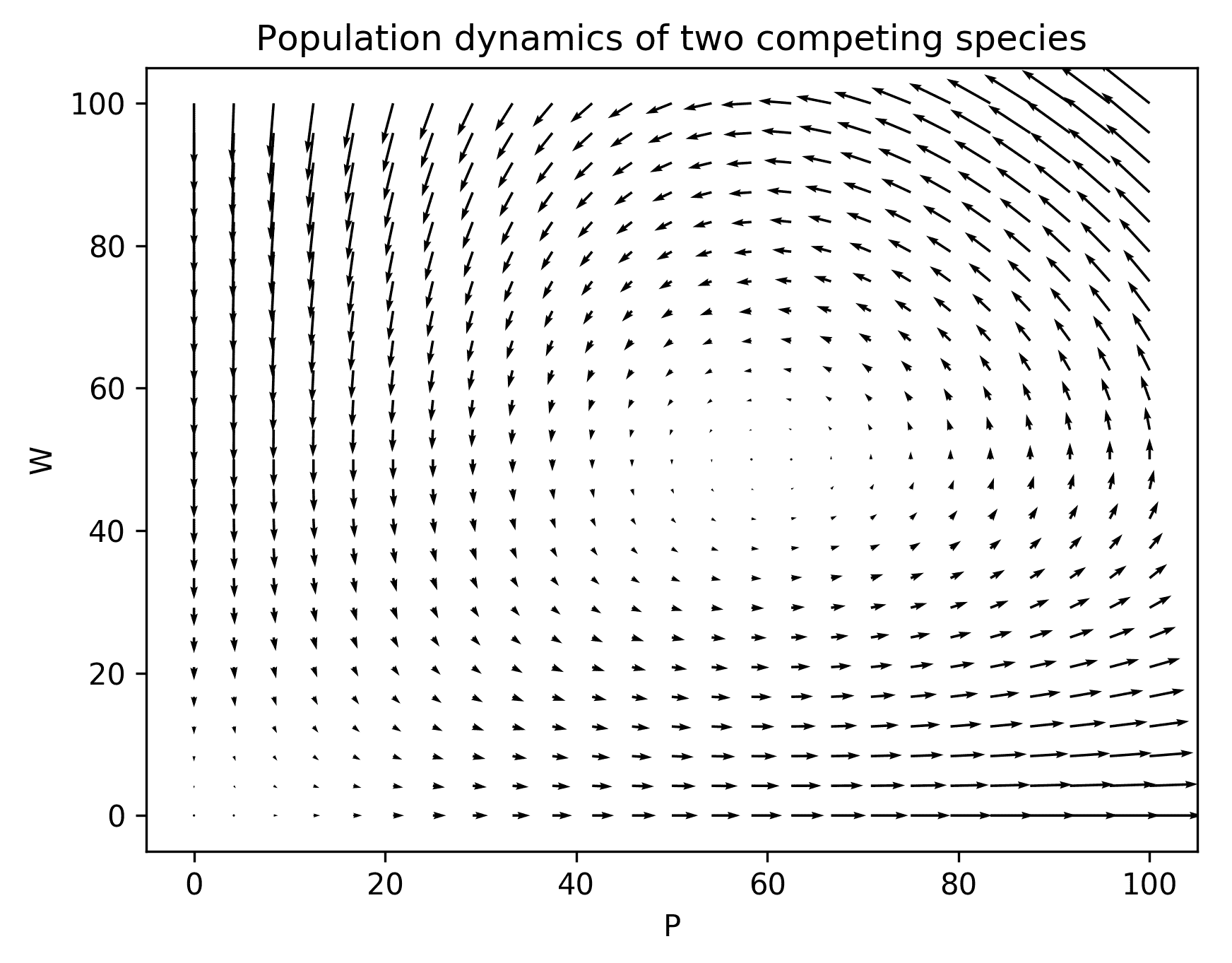
Figure 3.2: A quiver plot showing the population dynamics of two competing species modeled by a system of differential equations

为了更具体地理解解决方案，我们需要一些初始条件，以便我们可以使用前面配方中描述的solve_ivp例程。

5. 因为我们有两个方程，我们的初始条件将有两个值。（回想在文献[1]中，简单的微分方程数值求解 T2 公式，我们看到初始条件提供给一个 NUMPY 数组。）让我们考虑初始值 AUT3，P（0）＝85，T4 和 0。我们在 NumPy 数组中定义这些元素，并小心地将它们按正确的顺序放置：

initial_conditions = np.array([85, 40])

6. 现在我们可以使用scipy.integrate模块中的solve_ivp。我们需要提供max_step关键字参数，以确保我们在解决方案中有足够的点来提供平滑的解决方案曲线：

from scipy import integrate
sol = integrate.solve_ivp(predator_prey_system, (0., 5.),
   initial_conditions, max_step=0.01)

7. 让我们在现有图形上绘制此解决方案，以显示此特定解决方案与我们已经生成的方向图的关系。同时，我们还绘制了初始条件：

ax.plot(initial_conditions[0], initial_conditions[1], "ko")
ax.plot(sol.y[0, :], sol.y[1, :], "k", linewidth=0.5)

其结果如图 3.3所示：

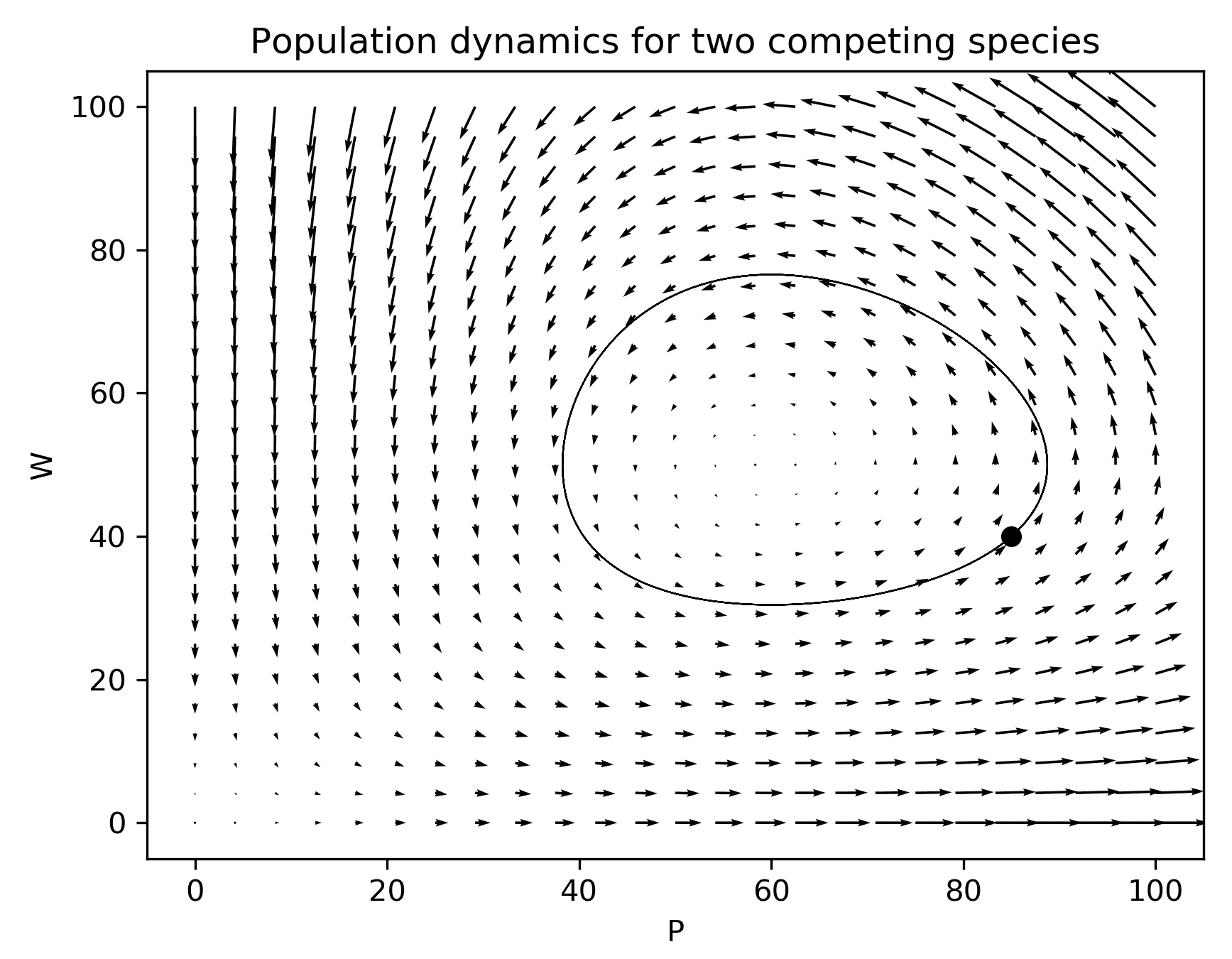
Figure 3.3: Solution trajectory plotted over a quiver plot showing the general behavior

它是如何工作的。。。

用于常微分方程组的方法与用于单个常微分方程的方法完全相同。我们首先把方程组写成一个单向量微分方程，

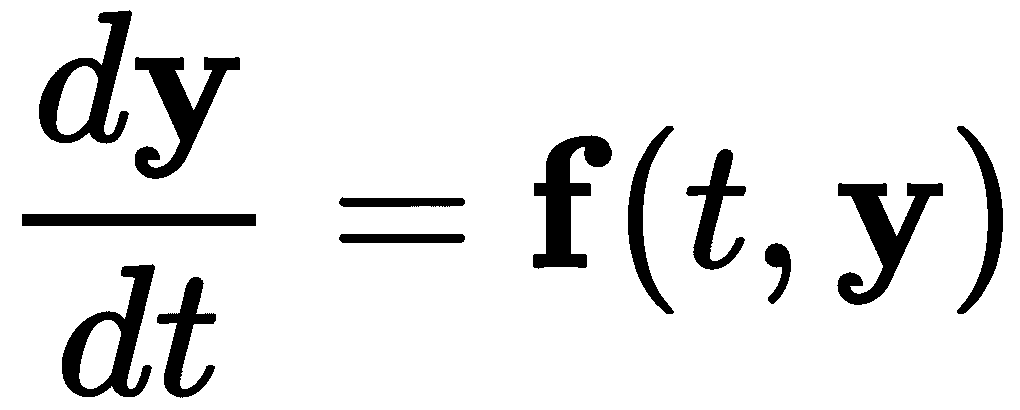
然后可以使用时间步进法来解决这个问题，就像y是一个简单的标量值一样。

使用quiver例程在平面上绘制方向箭头的技术是学习系统如何从给定状态演变的一种快速简便的方法。函数的导数表示曲线的梯度（x、u（x），因此微分方程描述了解函数在y位置和t时间的梯度。方程组描述了在给定位置y和时间t 处的独立解函数的梯度。当然，这个位置现在是一个二维点，所以当我们在一个点上绘制梯度时，我们将其表示为一个箭头，从该点开始，沿着梯度的方向。箭头的长度表示渐变的大小；箭头越长，解决方案曲线向该方向移动的“速度”越快。

当我们在这个方向场的顶部绘制解轨迹时，我们可以看到曲线（从点开始）遵循箭头指示的方向。解轨迹所示的行为是一个极限环，其中每个变量的解随着两个物种种群的增长或下降而呈周期性。如果我们将每个群体与时间进行对比，这种行为描述可能会更加清晰，如图 3.4所示。从图 3.3中不明显的是，溶液轨迹循环了好几次，但这在图 3.4中清楚地显示出来：

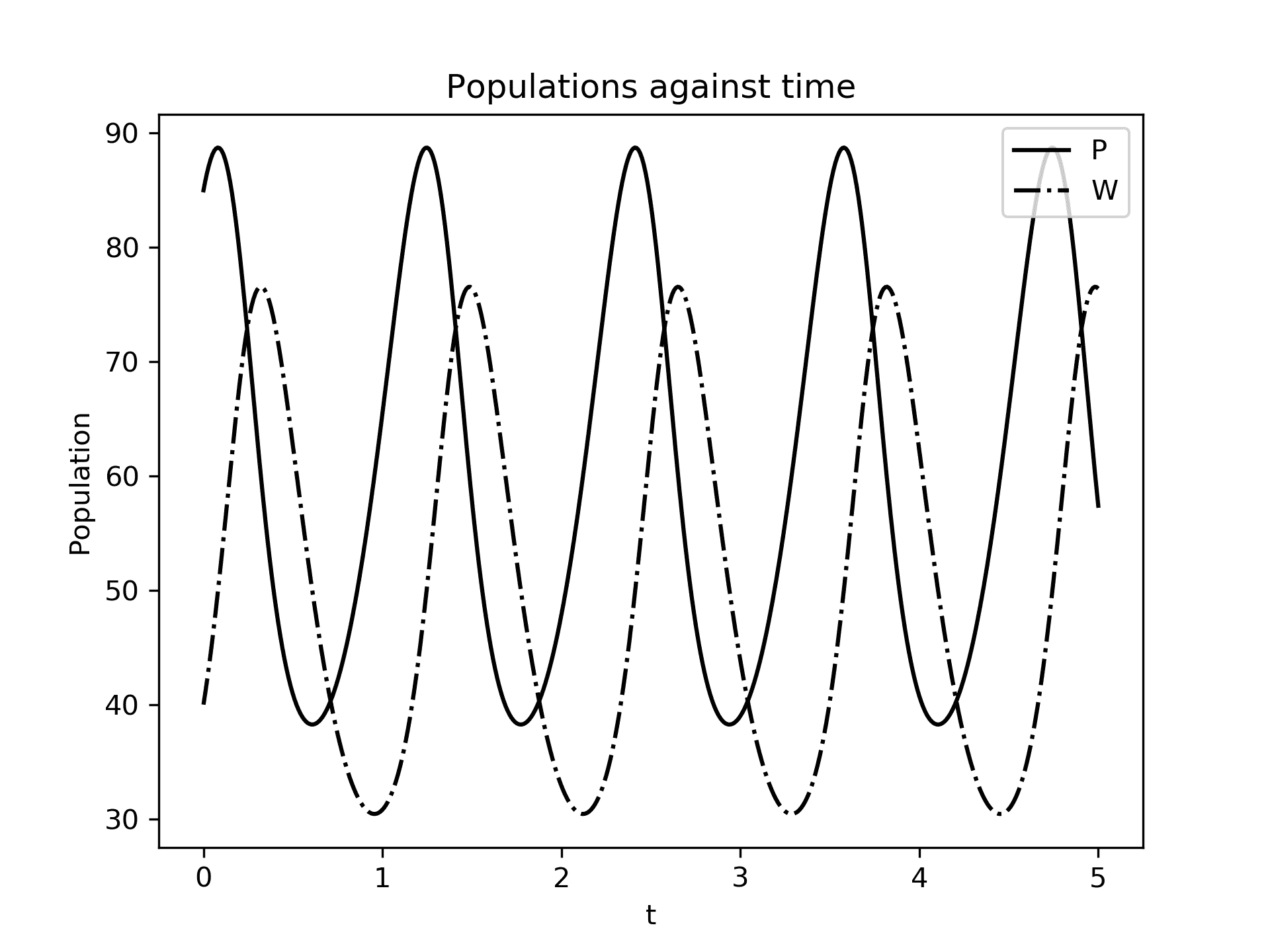
图 3.4：种群P和W随时间变化的曲线图。两个种群都表现出周期性行为

还有更多。。。

从各种初始条件开始，通过绘制变量之间的相对关系来分析常微分方程组的技术称为相空间（平面）分析。在此配方中，我们使用quiver绘图例程快速生成微分方程组的相平面近似值。通过分析微分方程组的相平面，我们可以识别解的不同局部和全局特征，例如极限环。

偏微分方程是涉及两个或多个变量中函数的偏导数的微分方程，与仅一个变量中的常导数相反。偏微分方程是一个广泛的话题，可以很容易地填满一系列的书。偏微分方程的一个典型例子是（一维）热方程

其中α为正常数，f（t，x为函数。该偏微分方程的解是一个函数u（t、x），它表示杆的温度，占据x范围 0≤ x≤ L，在给定时间t>0。为了简单起见，我们将取f（t、x）=0，即系统不进行加热/冷却，α=1，L=2。在实践中，我们可以重新缩放问题以修正常数α，因此这不是一个限制性问题。在本例中，我们将使用边界条件

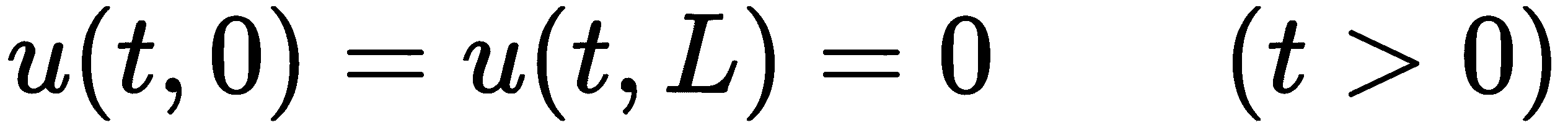
这相当于说，杆的两端保持在恒定温度 0。我们还将使用初始温度分布

该初始温度曲线描述了 0 和 2 之间的平滑曲线，峰值为 3，这可能是将中心棒加热至 3 的结果。

我们将使用一种称为有限差分的方法，我们将杆分成若干相等的段，将时间范围分成若干离散的步骤。然后，我们在每个分段和每个时间步计算解的近似值。

在本配方中，我们将使用有限差分法求解一个简单的偏微分方程。

准备

对于这个配方，我们需要 NumPy 包和 Matplotlib 包，像往常一样进口为np和plt。我们还需要从mpl_toolkits导入mplot3d模块，因为我们将生成一个 3D 绘图：

from mpl_toolkits import mplot3d

我们还需要 SciPy 包中的一些模块。

怎么做。。。

在以下步骤中，我们使用有限差分法求解热方程：

1. 让我们首先创建表示系统物理约束的变量：条的范围和α的值：

alpha = 1
x0 = 0 # Left hand x limit
xL = 2 # Right hand x limit

2. 我们首先将x范围划分为N相等的间隔，本例使用N+1点取N=10。我们可以使用 NumPy 的linspace例程生成这些点。我们还需要每个间隔的公共长度h:**

N = 10
x = np.linspace(x0, xL, N+1)
h = (xL - x0) / N

3. 接下来，我们需要设置时间方向上的步骤。我们在这里采取了稍微不同的方法；我们设置时间步长k和步数（隐式假设我们从时间 0 开始）：

k = 0.01
steps = 100
t = np.array([i*k for i in range(steps+1)])

4. 为了使该方法正常运行，我们必须

否则，系统可能会变得不稳定。我们将其左侧存储在一个变量中，以便在步骤 4中使用，并使用断言检查该不等式是否成立：

r = alpha*k / h**2
assert r < 0.5, f"Must have r < 0.5, currently r={r}"

5. 现在我们可以构造一个矩阵来保存有限差分格式中的系数。为此，我们使用scipy.sparse模块中的diags例程创建一个稀疏的三对角矩阵：

from scipy import sparse
diag = [1, *(1-2*r for _ in range(N-1)), 1]
abv_diag = [0, *(r for _ in range(N-1))]
blw_diag = [*(r for _ in range(N-1)), 0]

A = sparse.diags([blw_diag, diag, abv_diag], (-1, 0, 1), shape=(N+1,
      N+1), dtype=np.float64, format="csr")

6. 接下来，我们创建一个空白矩阵，用于保存解决方案：

u = np.zeros((steps+1, N+1), dtype=np.float64)

7. 我们需要将初始配置文件添加到第一行。最好的方法是创建一个保存初始配置文件的函数，并在我们刚刚创建的矩阵u中的x数组中存储对该函数求值的结果：

def initial_profile(x):
    return 3*np.sin(np.pi*x/2)

u[0, :] = initial_profile(x)

8. 现在我们可以简单地循环每一步，将A与前一行相乘，计算矩阵u的下一行：

for i in range(steps):
    u[i+1, :] = A @ u[i, :]

9. 最后，为了可视化我们刚刚计算的解决方案，我们可以使用 Matplotlib 将解决方案绘制为曲面：

X, T = np.meshgrid(x, t)
fig = plt.figure()
ax = fig.add_subplot(projection="3d")

ax.plot_surface(T, X, u, cmap="hot")
ax.set_title("Solution of the heat equation")
ax.set_xlabel("t")
ax.set_ylabel("x")
ax.set_zlabel("u")

其结果为图 3.5所示的曲面图：

图 3.5：0 范围内热方程解的曲面图≤ x≤ 2 使用有限差分法计算 10 个网格点

它是如何工作的。。。

有限差分法的工作原理是用一个简单的分数来代替每个导数，这个分数只涉及我们可以估计的函数值。为了实现这种方法，我们首先将空间范围和时间范围分解为若干离散区间，由网格点分隔。这个过程称为离散化。然后我们使用微分方程以及初始条件和边界条件来形成连续近似，其方式非常类似于数值求解微分方程配方中solve_ivp例程使用的时间步进方法。

为了解一个偏微分方程，比如热方程，我们至少需要三条信息。通常，对于热方程，其形式为空间维度的边界条件，告诉我们棒两端的行为，以及时间维度的初始条件，即棒上方的初始温度分布。

前面描述的有限差分方案通常称为前向时间中心空间（FTCS方案，因为我们使用前向有限差分来估计时间导数，中心有限差分来估计（二阶）空间导数。这些有限差分的公式如下所示：

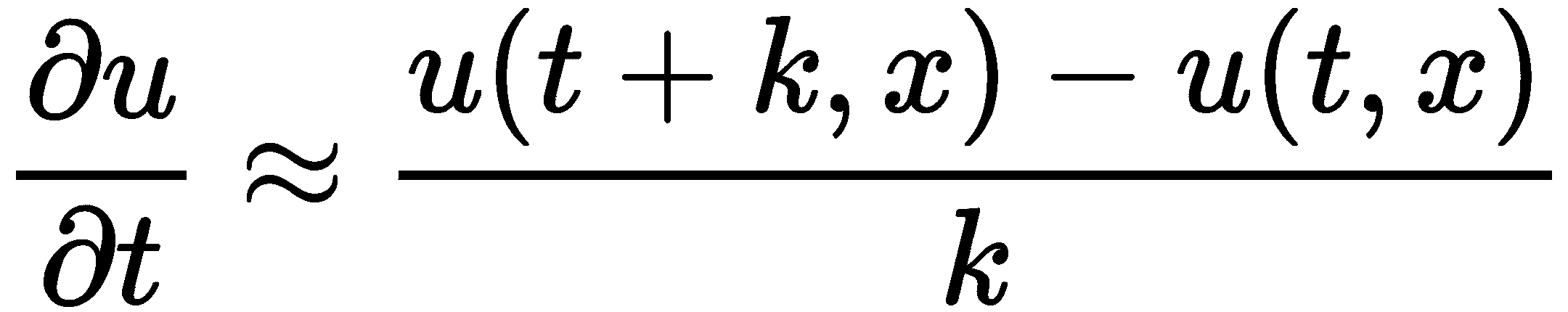
和

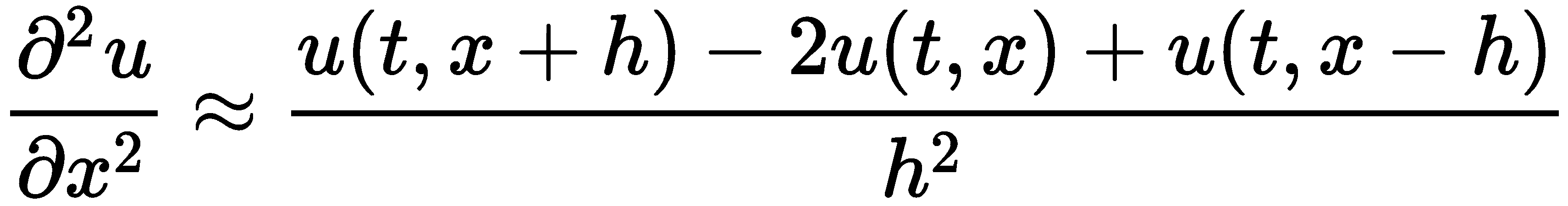
将这些近似值代入热方程，并在j之后使用u_i^j近似值作为*u*t_j、x_i的数值在i空间点的时间步长，我们得到

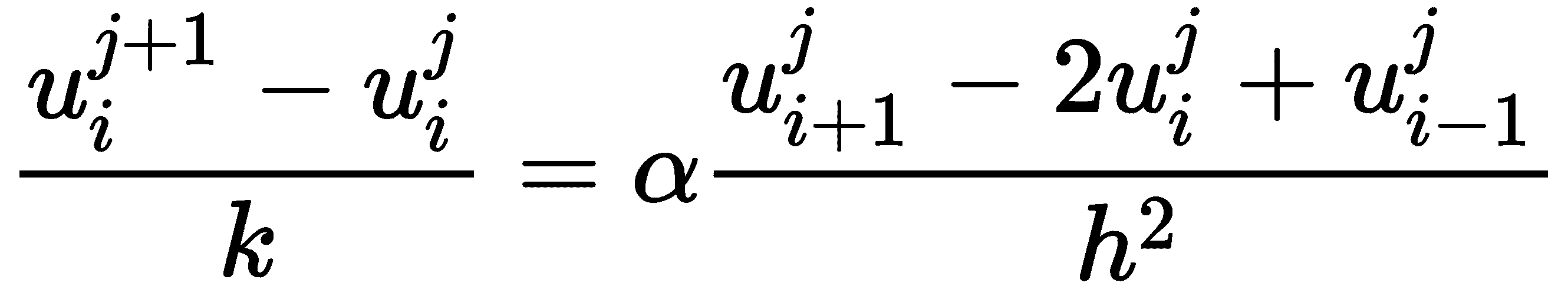
可以重新排列以获得公式

粗略地说，这个方程式表示，给定点的下一个温度取决于上一时刻周围的温度。这也说明了为什么需要对r值设置条件；如果条件不成立，右边的中间项将为负值。

我们可以把这个方程组写成矩阵形式，

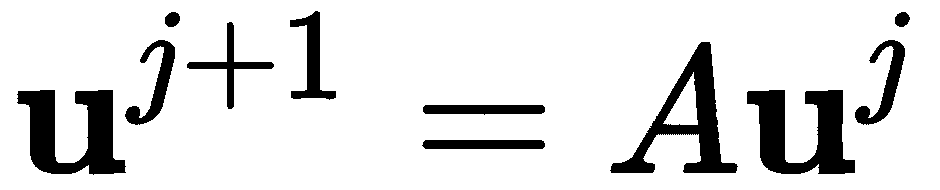
其中**u**j是包含步骤 4中定义的u_ij^j和矩阵a的近似值的向量。该矩阵是三对角的，这意味着非零项出现在前导对角线上或其附近。我们使用 SciPysparse模块中的diag例程，它是定义这类矩阵的实用工具。这与本章解方程配方中描述的过程非常相似。该矩阵的第一行和最后一行分别有零（左上角和右下角除外），表示（不变）边界条件。其他行的系数由微分方程任一侧导数的有限差分近似值给出。我们首先创建对角线条目以及对角线上方和下方的条目，然后使用diags例程创建稀疏矩阵。矩阵应该有N+1行和列，以匹配网格点的数量，我们将数据类型设置为双精度浮点和 CSR 格式。

初始轮廓为我们提供了向量u⁰，从第一点开始，我们可以通过简单地执行矩阵乘法来计算每个后续时间步，如步骤 7所示。

还有更多。。。

我们在这里描述的方法相当粗糙，因为正如我们所提到的，如果不小心控制时间步长和空间步长的相对大小，近似值可能会变得不稳定。此方法是显式，因为每个时间步仅使用来自前一时间步的信息显式计算。还有隐式方法，它们给出了一个方程组，可以通过求解得到下一个时间步长。不同的方案在解的稳定性方面具有不同的特点。

当函数f（t、x不是 0 时，我们可以通过使用赋值来轻松适应这种变化

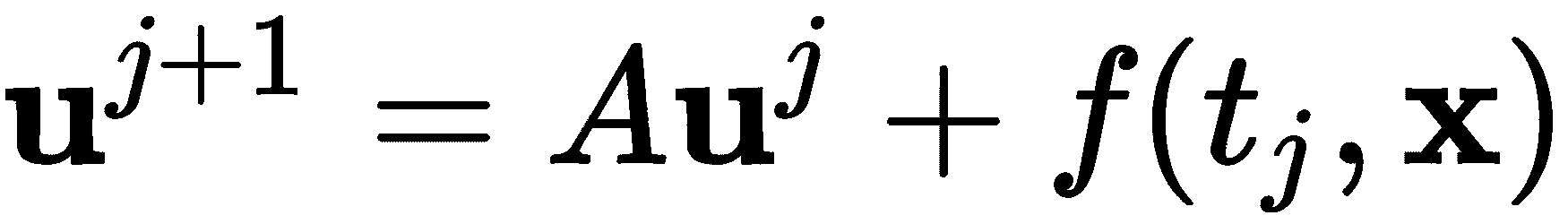
其中，函数被适当地矢量化，以使该公式有效。对于用于解决问题的代码，我们只需要包含函数的定义，然后按如下方式更改解决方案的循环：

for i in range(steps):
    u[i+1, :] = A @ u[i, :] + f(t[i], x)

从物理上讲，此函数表示沿杆的每个点处的外部热源（或散热器）。这可能会随着时间的推移而改变，这就是为什么一般情况下，函数应该同时使用t和x作为参数（尽管它们不需要同时使用）。

我们在本例中给出的边界条件表示保持恒定温度为 0 的杆端。这类边界条件有时称为Dirichlet边界条件。还有Neumann边界条件，其中函数u的导数在边界处给出。例如，我们可能已经得到了边界条件

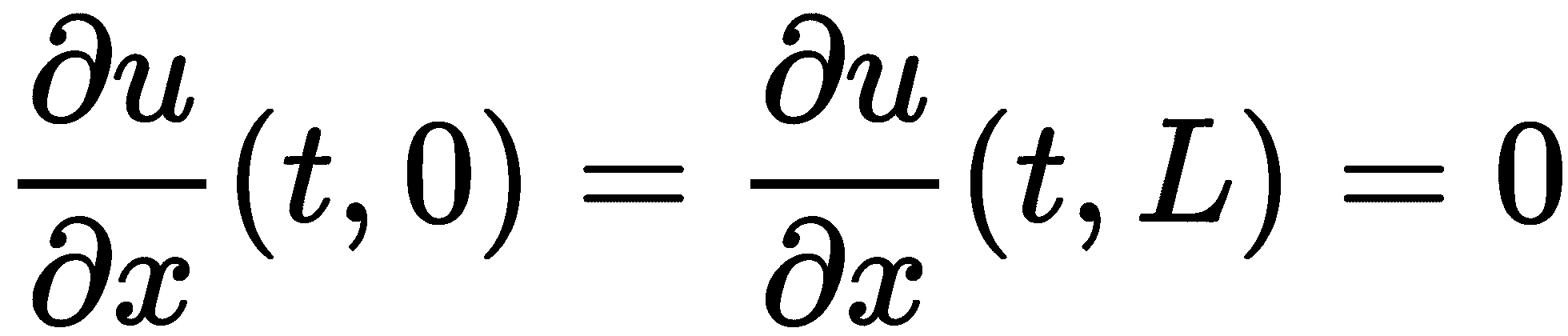
这在物理上可以解释为杆的端部被绝缘，因此热量不能通过端点逸出。对于这种边界条件，我们需要稍微修改矩阵A，但在其他情况下，方法保持不变。事实上，在边界左侧插入一个虚构的x值，并在左侧边界使用向后有限差分（x=0，我们得到

在二阶有限差分近似下，我们得到

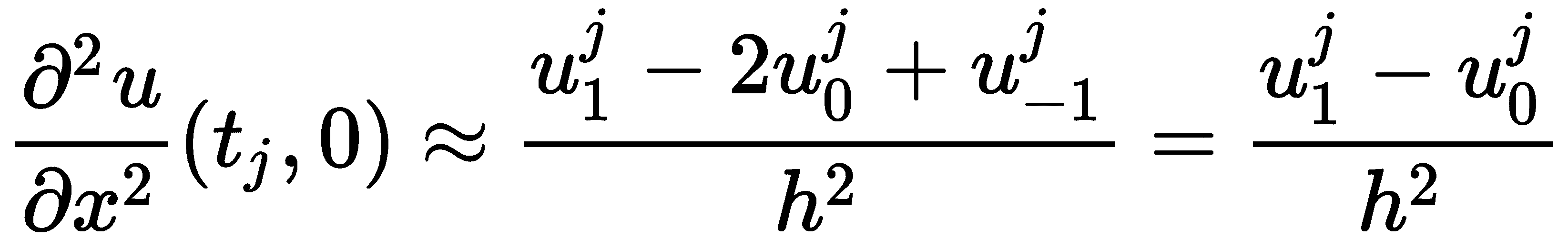
这意味着我们矩阵的第一行应该包含1-r、然后是r，然后是 0。对右侧极限使用类似的计算得出了矩阵的类似最后一行：

diag = [1-r, *(1-2*r for _ in range(N-1)), 1-r]
abv_diag = [*(r for _ in range(N))]
blw_diag = [*(r for _ in range(N))]

A = sparse.diags([blw_diag, diag, abv_diag], (-1, 0, 1), shape=(N+1, N+1), dtype=np.float64, format="csr")

对于涉及偏微分方程的更复杂问题，可能更适合使用有限元解算器。有限元法使用比偏微分方程更复杂的方法来计算解，偏微分方程通常比我们在本配方中看到的有限差分法更灵活。然而，这是以需要更多依赖于更先进数学理论的设置为代价的。另一方面，有一个 Python 包，用于使用 FEniCS 等有限元方法求解偏微分方程（fenicsproject.org）。使用 FEniCS 这样的软件包的优点是，它们通常会根据性能进行调整，这在高精度解决复杂问题时非常重要。

另见

FEniCS 文档很好地介绍了有限元方法以及使用该软件包求解各种经典偏微分方程的一些示例。下一本书对该方法和理论进行了更全面的介绍：

• Johnson，C.（2009）。偏微分方程的有限元数值解。纽约州米诺拉：多佛出版社。

有关如何使用 Matplotlib 生成三维曲面图的更多详细信息，请参见第 2 章中的曲面和等高线图配方，以及使用 Matplotlib 进行的数学绘图。

微积分中最有用的工具之一是*傅里叶变换m。粗略地说，傅里叶变换以可逆的方式改变了某些函数的表示。这种表示形式的变化在处理表示为时间函数的信号时特别有用。在这种情况下，傅里叶变换将信号表示为频率的函数；我们可以将其描述为从信号空间到频率空间的转换。这可用于识别信号中存在的频率，以进行识别和其他处理。实际上，我们通常会对信号进行离散采样，因此我们必须使用离散傅里叶变换*来执行此类分析。幸运的是，有一种计算效率高的算法，称为*快速傅里叶变换（FFT），用于将离散傅里叶变换应用于样本。*

*我们将遵循使用 FFT 过滤噪声信号的通用过程。第一步是应用 FFT 并使用数据计算信号的功率谱密度。然后，我们识别峰值并过滤掉对信号没有足够大贡献的频率。然后应用逆 FFT 得到滤波后的信号。

在此配方中，我们使用 FFT 分析信号样本，识别存在的频率，并清除信号中的噪声。

准备

对于这个配方，我们只需要像往常一样将 NumPy 和 Matplotlib 包作为np和plt导入。

怎么做。。。

按照以下说明使用 FFT 处理噪声信号：

1. 我们定义了一个函数，该函数将生成我们的基本信号：

def signal(t, freq_1=4.0, freq_2=7.0):
    return np.sin(freq_1 * 2 * np.pi * t) + np.sin(freq_2 * 2 *
        np.pi * t)

2. 接下来，我们通过向基础信号添加一些高斯噪声来创建样本信号。我们还创建了一个数组，用于保存样本t值处的真实信号，以方便以后使用：

state = np.random.RandomState(12345)
sample_size = 2**7 # 128
sample_t = np.linspace(0, 4, sample_size)
sample_y = signal(sample_t) + state.standard_normal(sample_size)
sample_d = 4./(sample_size - 1) # Spacing for linspace array
true_signal = signal(sample_t)

3. 我们使用 NumPy 的fft模块来计算离散傅里叶变换。在开始分析之前，我们从 NumPy 导入以下内容：

from numpy import fft

4. 要查看噪声信号的外观，我们可以绘制叠加真实信号的采样信号点：

fig1, ax1 = plt.subplots()
ax1.plot(sample_t, sample_y, "k.", label="Noisy signal")
ax1.plot(sample_t, signal(sample_t), "k--", label="True signal")

ax1.set_title("Sample signal with noise")
ax1.set_xlabel("Time")
ax1.set_ylabel("Amplitude")
ax1.legend()

此处创建的图如图 3.6所示。如我们所见，噪声信号与真实信号不太相似（用虚线显示）：

图 3.6：真实信号叠加的噪声信号样本

5. 现在，我们将使用离散傅里叶变换来提取样本信号中存在的频率。fft模块中的fft例程执行 FFT（离散傅里叶变换）：

spectrum = fft.fft(sample_y)

6. fft模块提供一个例程，用于构造称为fftfreq的适当频率值。为方便起见，我们还生成一个数组，其中包含正频率出现的整数：

freq = fft.fftfreq(sample_size, sample_d)
pos_freq_i = np.arange(1, sample_size//2, dtype=int)

7. 接下来，计算信号的功率谱密度（PSD），如下：

psd = np.abs(spectrum[pos_freq_i])**2 + np.abs(spectrum[-
        pos_freq_i])**2

8. 现在，我们可以绘制正频率信号的 PSD，并使用此图识别频率：

fig2, ax2 = plt.subplots()
ax2.plot(freq[pos_freq_i], psd)
ax2.set_title("PSD of the noisy signal")
ax2.set_xlabel("Frequency")
ax2.set_ylabel("Density")

结果见图 3.7。我们可以在这张图中看到，大约在 4 和 7 处有尖峰，这是我们前面定义的信号频率：

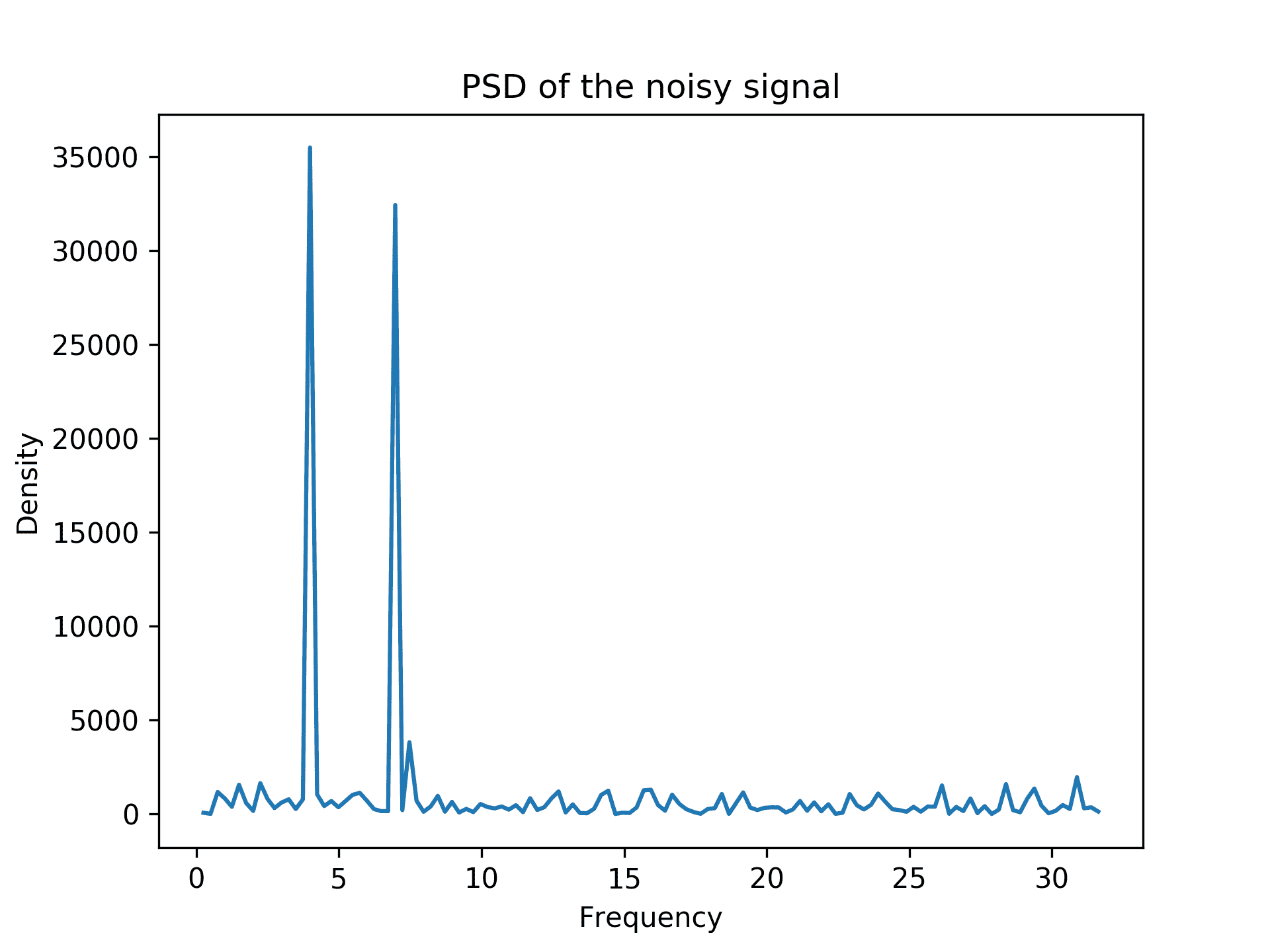
图 3.7:FFT 生成信号的功率谱密度

9. 我们可以识别这两个频率，尝试从噪声样本中重建真实信号。出现的所有次要峰值都不大于 10000，因此我们可以将其用作过滤器的截止值。现在，让我们从所有正频率指数列表中提取对应于 PSD 中 10000 以上峰值的指数（希望有 2 个）：

filtered = pos_freq_i[psd > 1e4]

10. 接下来，我们创建一个新的、干净的频谱，它只包含我们从噪声信号中提取的频率。我们通过创建一个只包含 0 的数组来实现这一点，然后从对应于滤波频率及其负数的索引中复制spectrum的值：

new_spec = np.zeros_like(spectrum)
new_spec[filtered] = spectrum[filtered]
new_spec[-filtered] = spectrum[-filtered]

11. 现在，我们使用逆 FFT（使用ifft例程）将这个干净的频谱转换回原始样本的时域。我们使用 NumPy 的real例程获取实部，以消除错误的虚部：

new_sample = np.real(fft.ifft(new_spec))

12. 最后，我们将该滤波信号绘制在真实信号上，并比较结果：

fig3, ax3 = plt.subplots()
ax3.plot(sample_t, true_signal, color="#8c8c8c", linewidth=1.5, label="True signal")
ax3.plot(sample_t, new_sample, "k--", label="Filtered signal")
ax3.legend()
ax3.set_title("Plot comparing filtered signal and true signal")
ax3.set_xlabel("Time")
ax3.set_ylabel("Amplitude")

步骤 12的结果如图 3.8所示。我们可以看到，滤波后的信号与真实信号非常匹配，除了一些小的差异：

图 3.8：使用 FFTs 和滤波生成的滤波信号与真实信号的对比图

它是如何工作的。。。

函数f（t的傅里叶变换由积分给出

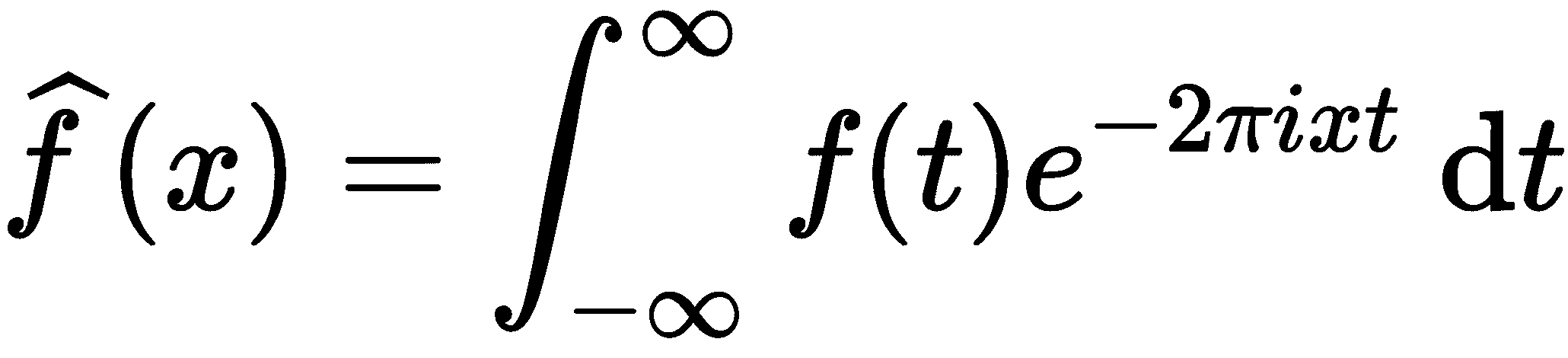
离散傅里叶变换由下式给出

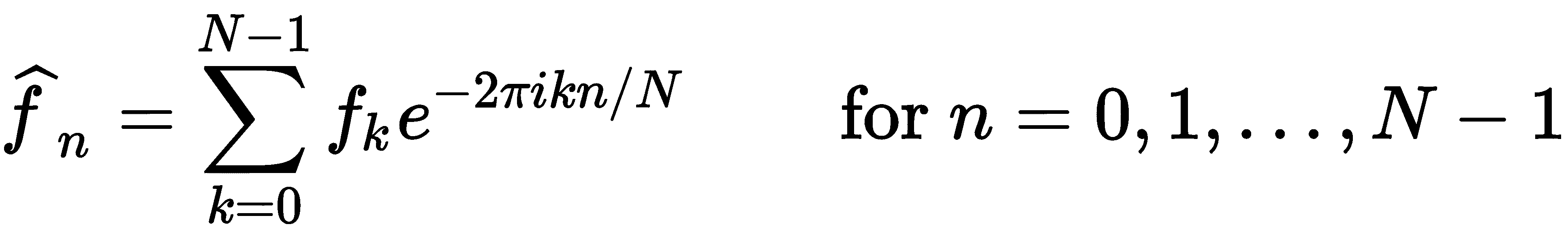
这里，f_k值是作为复数的样本值。离散傅里叶变换可以使用前面的公式计算，但在实践中这是无效的。使用此公式计算为O（N²）。FFT 算法将复杂度提高到了O（NlogN，这是非常好的。数字配方一书（在进一步阅读一节中给出了完整的书目细节）对 FFT 算法和离散傅里叶变换进行了非常好的描述。

我们将对已知信号（具有已知频率模式）生成的样本应用离散傅里叶变换，以便我们可以看到我们获得的结果与原始信号之间的联系。为了保持该信号的简单性，我们创建了一个只有两个频率分量的信号，其值分别为 4 和 7。根据这个信号，我们生成了我们分析的样本。由于 FFT 的工作方式，最好样本大小为 2 的幂；如果不是这样，我们可以用零元素填充样本，使其成为现实。我们在样本信号中加入一些高斯噪声，这种噪声的形式是正态分布的随机数。

fft例程返回的数组包含N+1元素，其中N为样本量。索引 0 对应的元素是 0 频率或 DC 移位。接下来的N/2元素是对应于正频率的值，最后的N/2元素是对应于负频率的值。频率的实际值由采样点N的数量和样本间距确定，在本例中，样本间距存储在sample_d中。

频率ω处的功率谱密度由公式给出

其中，H（ω表示频率ω处信号的傅里叶变换。功率谱密度测量每个频率对整个信号的贡献，这就是为什么我们在大约 4 和 7 处看到峰值。由于 Python 索引允许我们对从序列末尾开始的元素使用负索引，因此我们可以使用正索引数组从spectrum获取正频率元素和负频率元素。

在步骤 9 中，我们提取了曲线图上峰值在 10000 以上的两个频率的指数。与这些指数相对应的频率为 3.984375 和 6.97265625，它们并不完全等于 4 和 7，但非常接近。产生这种差异的原因是，我们使用有限数量的点对连续信号进行采样。（当然，使用更多的点会产生更好的近似值。）

在步骤 11中，我们取逆 FFT 返回的数据的实部。这是因为，从技术上讲，FFT 处理复杂数据。因为我们的数据只包含真实数据，所以我们希望这个新信号也应该只包含真实数据。然而，会有一些小错误，这意味着结果并不完全真实。我们可以通过取逆 FFT 的实部来解决这个问题。这是合适的，因为我们可以看到虚部非常小。

我们可以在图 3.8中看到，滤波后的信号与真实信号非常接近，但并不精确。这是因为，如前所述，我们用相对较小的样本近似连续信号。

还有更多。。。

生产环境中的信号处理可能会使用专门的软件包，例如来自scipy的signal模块，或一些较低级别的代码或硬件来执行信号过滤或清理。这个方法应该更多地被看作是一个使用 FFT 作为处理从某种基本周期结构（信号）采样的数据的工具的演示。FFT 对于求解偏微分方程非常有用，如数值求解偏微分方程配方中的热方程。

另见

有关随机数和正态分布（高斯）的更多信息，请参见第 4 章、处理随机性和概率。

微积分是每一门本科数学课程的重要组成部分。有许多关于微积分的优秀教科书，包括斯皮瓦克的经典教科书和亚当斯和埃塞克斯的更全面的课程：

• 斯皮瓦克，M.（2006）。微积分第三版剑桥：剑桥大学出版社
• 亚当斯，R.和埃塞克斯，C.（2018）。微积分：一门完整的课程。第 9 版，唐·米尔斯，安大略省：皮尔逊。瓜西安

数值微分和积分的一个很好的来源是经典的 To.T0 数值公式损坏 T1 书籍，它全面地描述了如何解决 C++中的许多计算问题，包括理论的总结：

• *出版社，W.，Teukolsky，S.，Vetterling，W.和 Flannery，B.（2007）。数字配方：**科学计算的艺术。第三版剑桥：剑桥大学出版社*****