关注我们

回归算法中的多元线性回归函数

简单线性回归的扩展使用两个或多个特征预测响应。数学上，无涯教程可以解释如下-

考虑一个具有 n 个观察值， p 个特征(即自变量)和 y 个作为一个响应的数据集，即因变量，可以计算出p个特征的回归线如下-

无涯教程网

h(xi)=b0+b1xi1+b2xi2+⋯+bpxip

在此，h(xi)是预测的响应值，回归系数: $b_{0} ， b_{1} ， b_{2} ， \dots b_{p}$

多个线性回归模型始终将数据中的误差称为残留误差,该误差会按以下方式更改计算:

h(xi)=b0+b1xi1+b2xi2+⋯+bpxip+ei

还可以将上面的等式写成如下-

yi=h(xi)+eiorei=yi-h(xi)

Python代码实现

在此示例中，无涯教程将使用scikit learning的Boston住房数据集-

首先，将从导入必要的包开始，如下所示:

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metrics

接下来，按如下方式加载数据集-

boston=datasets.load_boston(return_X_y=False)

以下脚本行将定义特征矩阵X和响应向量Y-

X=boston.data
y=boston.target

接下来，将数据集分为训练集和测试集，如下所示:

链接：https://www.learnfk.comhttps://www.learnfk.com/python-machine-learning/machine-learning-with-python-multiple-linear-regression.html

来源：LearnFk无涯教程网

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test=train_test_split(X, y, test_size=0.7, random_state=1)

现在，创建线性回归对象并按如下所示训练模型-

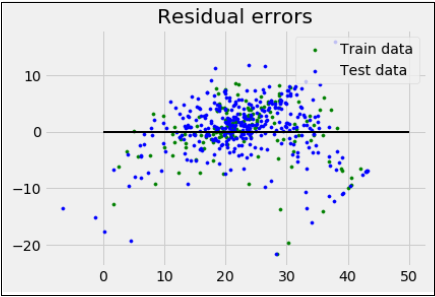
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients:\n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train, color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test, color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()

输出

Coefficients:
[-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00 -1.77862563e+01 
   2.80392779e+00 4.61905315e-02 -1.13518865e+00 3.31725870e-01 -1.01196059e-02 
   -9.94812678e-01 9.18522056e-03 -7.92395217e-01]
Variance score: 0.709454060230326