- PHP7 数据结构和算法

PHP 使用先进技术解决问题详解
到目前为止,我们在本书中探讨了不同的数据结构和算法。我们还需要探索一些最令人兴奋的算法领域。在计算机编程中有很多有效的方法。在本章中,我们将重点介绍一些关键的高级技术和概念。这些主题非常重要,可以单独写一本关于它们的书。然而,我们将把重点放在对这些高级主题的基本理解上。当我们提到高级主题时,我们指的是记忆、动态规划、贪婪算法、回溯、解谜、机器学习等等。让我们在以下部分学习一些新的和令人兴奋的主题。
记忆是一种优化技术,我们可以存储以前昂贵操作的结果,并在不重复操作的情况下使用它们。它帮助我们大大加快了解决方案的速度。当我们遇到重复子问题的问题时,我们可以轻松地应用此技术来存储这些结果,并在以后使用它们,而无需重复这些步骤。由于 PHP 非常支持关联数组和动态数组属性,因此我们可以毫无问题地缓存结果。我们必须记住的一点是,尽管我们通过缓存结果来节省时间,但我们需要更多的内存来将这些结果存储在缓存中。因此,我们必须在空间和内存之间进行权衡。现在,让我们重温第 5 章应用递归算法——递归,以获取生成斐波那契数的递归示例。我们将使用计数器修改该函数,以了解调用该函数的次数以及函数的运行时间,从而获得第三十个斐波那契数。以下是此操作的代码:
$start Time = microtime();
$count = 0;
function fibonacci(int $n): int {
global $count;
$count++;
if ($n == 0) {
return 1;
} else if ($n == 1) {
return 1;
} else {
return fibonacci($n - 1) + fibonacci($n - 2);
}
}
echo fibonacci(30) . "\n";
echo "Function called: " . $count . "\n";
$endTime = microtime();
echo "time =" . ($endTime - $startTime) . "\n";
这将在命令行中具有以下输出。请注意,时间和结果可能因系统而异,也可能因 PHP 的不同版本而异。这完全取决于程序运行的位置:
1346269
Function called: 2692537
time =0.531349
第一个数字 1346269 是第三十个斐波那契数,下一行显示在生成第三十个数字的过程中,fibonacci函数被调用了 2692537 次。整个过程耗时 0.5 秒(我们使用的是 PHP 的microtime函数)。如果我们生成第五十个斐波那契数,函数调用计数将超过 400 亿次。这是一个很大的数字。然而,我们从斐波那契公式中知道,当我们计算n时。我们是通过n1 和n2 进行的;这些已经在前面的步骤中进行了计算。因此,我们正在重复这些步骤,因此,这将耗费我们的时间和效率。现在,让我们将斐波那契结果存储在一个索引数组中,我们将检查我们要查找的斐波那契数是否已经计算出来。如果是计算出来的,我们就用它,;否则,我们将计算并存储结果。下面是使用相同的递归过程生成斐波那契数的修改代码,但需要借助记忆:
$startTime = microtime();
$fibCache = [];
$count = 0;
function fibonacciMemoized(int $n): int {
global $fibCache;
global $count;
$count++;
if ($n == 0 || $n == 1) {
return 1;
} else {
if (isset($fibCache[$n - 1])) {
$tmp = $fibCache[$n - 1];
} else {
$tmp = fibonacciMemoized($n - 1);
$fibCache[$n - 1] = $tmp;
}
if (isset($fibCache[$n - 2])) {
$tmp1 = $fibCache[$n - 2];
} else {
$tmp1 = fibonacciMemoized($n - 2);
$fibCache[$n - 2] = $tmp1;
}
return $tmp + $tmp1;
}
}
echo fibonacciMemoized(30) . "\n";
echo "Function called: " . $count . "\n";
$endTime = microtime();
echo "time =" . ($endTime - $startTime) . "\n";
从前面的代码中可以看出,我们引入了一个新的全局变量$fibCache,它将存储计算出的斐波那契数。我们还检查我们要查找的数字是否已经在数组中。如果数字已经存储在缓存数组中,则不计算斐波那契。如果现在运行此代码,我们将看到以下输出:
1346269
Function called: 31
time =5.299999999997E-5
现在,让我们检查一下结果。第三十个斐波那契数和上次的一样。但是,请查看函数调用计数。这仅仅是 31 次,而不是 270 万次。现在,让我们看看时间。我们只花了 0.00005299 秒,比非记忆版本快 10000 倍。
通过一个简单的例子,我们可以看到,我们可以通过在适用的地方利用记忆来优化我们的解决方案。有一件事我们必须记住的是记忆化将更好地工作在我们重复子问题或我们必须考虑以前的计算来计算当前或未来的计算。尽管内存化会占用额外的空间来存储部分计算的数据,但使用内存化可以大幅度提高性能
模式匹配是我们日常执行的最常见的任务之一。PHP 内置了对正则表达式的支持,我们主要依靠正则表达式和内置字符串函数来解决此类问题的常规需求。PHP 有一个名为strops的现成函数,它返回字符串在文本中第一次出现的位置。因为它只返回第一次出现的位置,所以我们可以尝试编写一个函数来返回所有可能的位置。我们将首先探索蛮力方法,在这里,我们将使用每个模式字符串检查每个字符的实际字符串。以下是将为我们完成这项工作的功能:
function strFindAll(string $pattern, string $txt): array {
$M = strlen($pattern);
$N = strlen($txt);
$positions = [];
for ($i = 0; $i <= $N - $M; $i++) {
for ($j = 0; $j < $M; $j++)
if ($txt[$i + $j] != $pattern[$j])
break;
if ($j == $M)
$positions[] = $i;
}
return $positions;
}
方法非常简单。我们从实际字符串的位置 0 开始,一直到$N-$M位置,其中$M是我们要寻找的图案的长度。即使在模式不匹配的最坏情况下,我们也不需要搜索完整字符串。现在,让我们用一些参数调用函数:
$txt = "AABAACAADAABABBBAABAA";
$pattern = "AABA";
$matches = strFindAll($pattern, $txt);
if ($matches) {
foreach ($matches as $pos) {
echo "Pattern found at index : " . $pos . "\n";
}
}
这将产生以下输出:
Pattern found at index : 0
Pattern found at index : 9
Pattern found at index : 16
如果我们看我们的$txt字符串,我们可以发现我们的模式AABA.有树出现,第一个在开始,第二个在中心,第三个接近字符串的结尾。我们编写的算法将采用O((N - M) * M)复杂度,其中 N 是文本的长度,M 是我们正在搜索的模式的长度。如果我们愿意,我们可以使用一种被称为Knuth Morris Pratt(KMP字符串匹配算法)的流行算法来提高这种匹配的效率。
Knuth-Morris-Pratt(KMP)字符串匹配算法与我们刚刚实现的朴素算法非常相似。基本区别在于 KMP 算法使用部分匹配的信息,并决定在任何不匹配时停止匹配。它还可以预先计算模式可能存在的位置,以便减少重复比较或错误检查的数量。KMP 算法预先计算一个表,该表在搜索操作期间有助于提高效率。在实现 KMP 算法时,我们需要计算最长的正确前缀后缀(LPS。让我们检查生成 LPS 部件的函数:
function ComputeLPS(string $pattern, array &$lps) {
$len = 0;
$i = 1;
$M = strlen($pattern);
$lps[0] = 0;
while ($i < $M) {
if ($pattern[$i] == $pattern[$len]) {
$len++;
$lps[$i] = $len;
$i++;
} else {
if ($len != 0) {
$len = $lps[$len - 1];
} else {
$lps[$i] = 0;
$i++;
}
}
}
}
对于前面示例 AABA 中的模式,LPS 将为[0,1,0,1];现在,让我们为字符串/模式搜索问题编写 KMP 实现:
function KMPStringMatching(string $str, string $pattern): array {
$matches = [];
$M = strlen($pattern);
$N = strlen($str);
$i = $j = 0;
$lps = [];
ComputeLPS($pattern, $lps);
while ($i < $N) {
if ($pattern[$j] == $str[$i]) {
$j++;
$i++;
}
if ($j == $M) {
array_push($matches, $i - $j);
$j = $lps[$j - 1];
} else if ($i < $N && $pattern[$j] != $str[$i]) {
if ($j != 0)
$j = $lps[$j - 1];
else
$i = $i + 1;
}
}
return $matches;
}
前面的代码是 KMP 算法的实现。现在,让我们使用实现的算法运行以下示例:
$txt = "AABAACAADAABABBBAABAA";
$pattern = "AABA";
$matches = KMPStringMatching($txt, $pattern);
if ($matches) {
foreach ($matches as $pos) {
echo "Pattern found at index : " . $pos . "\n";
}
}
这将产生以下输出:
Pattern found at index : 0
Pattern found at index : 9
Pattern found at index : 16
KMP 算法的复杂度为O(N + M),远优于常规模式匹配。这里,O (M)用于计算 LPS,O (N)用于 KMP 算法本身。
There are many detailed descriptions of the KMP algorithm that can be found online.
虽然名字叫贪婪算法,但实际上,它是一种编程技术,专注于在给定时刻找出最佳可能的解决方案。这意味着贪婪算法做出了一个局部最优选择,希望它能得到全局最优解。我们必须记住的一点是,并不是所有贪婪的方法都能让我们找到全局最优的解决方案。然而,贪婪算法仍然被应用于许多问题求解领域。贪婪算法最常用的用途之一是在哈夫曼编码中,哈夫曼编码用于对大文本进行编码,并通过将它们转换为不同的代码来压缩字符串。我们将在下一节探讨哈夫曼编码的概念和实现。
哈夫曼编码是一种压缩技术,用于减少发送或存储消息或字符串所需的位数。它基于这样一种思想:频繁出现的字符将具有较短的位表示,而频率较低的字符将具有较长的位表示。如果我们将赫夫曼编码视为树结构,那么较不频繁的字符或项将位于树的顶部,更频繁的项将位于树的底部或叶中。哈夫曼编码在很大程度上依赖于优先级队列。哈夫曼编码可以通过首先创建一个节点树来计算。
创建节点树的过程:
- 我们必须为每个符号创建一个叶节点,并将其添加到优先级队列中。
- 当队列中有多个节点时,请执行以下操作:
1.移除最高优先级(最低概率/频率)的节点两次,以获得两个节点。
2.创建一个新的内部节点,将这两个节点作为子节点,其概率/频率等于两个节点的概率/频率之和。
3.将新节点添加到队列中。
- 剩下的节点是根节点,树就完成了。
然后,我们必须从根到叶遍历构造的二叉树,在每个节点上为一个分支分配和累积“0”,为另一个分支分配和累积“1”。每个叶子上累积的 0 和 1 构成了这些符号和权重的哈夫曼编码。以下是使用 SPL 优先级队列的哈夫曼编码算法的实现:
function huffmanEncode(array $symbols): array {
$heap = new SplPriorityQueue;
$heap->setExtractFlags(SplPriorityQueue::EXTR_BOTH);
foreach ($symbols as $symbol => $weight) {
$heap->insert(array($symbol => ''), -$weight);
}
while ($heap->count() > 1) {
$low = $heap->extract();
$high = $heap->extract();
foreach ($low['data'] as &$x)
$x = '0' . $x;
foreach ($high['data'] as &$x)
$x = '1' . $x;
$heap->insert($low['data'] + $high['data'],
$low['priority'] + $high['priority']);
}
$result = $heap->extract();
return $result['data'];
}
这里,我们为每个符号构建一个最小堆,并使用它们的权重来设置优先级。一旦构建了堆,我们将一个接一个地提取两个节点,并结合它们的数据和优先级将它们添加回堆中。除非只有一个节点(根节点)存在,否则此操作将继续。现在,让我们运行以下代码来生成哈夫曼代码:
$txt = 'PHP 7 Data structures and Algorithms';
$symbols = array_count_values(str_split($txt));
$codes = huffmanEncode($symbols);
echo "Symbol\t\tWeight\t\tHuffman Code\n";
foreach ($codes as $sym => $code) {
echo "$sym\t\t$symbols[$sym]\t\t$code\n";
}
在这里,我们使用str_split将字符串分解为一个数组,然后使用数组计数值将其转换为一个关联数组,其中字符将是键,其在字符串中的出现次数将是值。上述代码将产生以下输出:
Symbol Weight Huffman Code
i 1 00000
D 1 00001
d 1 00010
A 1 00011
t 4 001
H 1 01000
m 1 01001
P 2 0101
g 1 01100
o 1 01101
e 1 01110
n 1 01111
7 1 10000
l 1 10001
u 2 1001
5 101
h 1 11000
c 1 11001
a 3 1101
r 3 1110
s 3 1111
贪婪算法还有许多其他实际用途。我们将用贪婪算法解决一个作业调度问题。让我们考虑一组敏捷软件开发人员的例子,他们正在进行为期两周的迭代或冲刺。他们有一些用户故事需要完成,还有一些任务的截止日期(按日期)和故事的速度(故事的大小)。团队的目标是在给定的最后期限内获得冲刺的最大速度。让我们考虑下列任务:截止日期和速度:
| 指标 | 1. | 2. | 3. | 4. | 5. | 6. | | 故事 | S1 | S2 | S3 | S4 | S5 | 中六 | | 截止日期 | 2. | 1. | 2. | 1. | 3. | 4. | | 速度 | 95 | 32 | 47 | 42 | 28 | 64 |
从上表可以看出,我们有六个用户案例,它们有四个不同的截止日期,从1到4。我们必须完成插槽 1 的用户故事S2或S4,因为任务的截止日期是 1。故事S1和S3也是如此,它们必须在插槽2上或之前完成。但是,由于我们有S3并且S3的速度大于S2和S4,因此将通过贪婪方法为插槽 1 选择 S3。让我们为速度计算编写贪婪代码:
function velocityMagnifier(array $jobs) {
$n = count($jobs);
usort($jobs, function($opt1, $opt2) {
return $opt1['velocity'] < $opt2['velocity'];
});
$dMax = max(array_column($jobs, "deadline"));
$slot = array_fill(1, $dMax, -1);
$filledTimeSlot = 0;
for ($i = 0; $i < $n; $i++) {
$k = min($dMax, $jobs[$i]['deadline']);
while ($k >= 1) {
if ($slot[$k] == -1) {
$slot[$k] = $i;
$filledTimeSlot++;
break;
}
$k--;
}
if ($filledTimeSlot == $dMax) {
break;
}
}
echo("Stories to Complete: ");
for ($i = 1; $i <= $dMax; $i++) {
echo $jobs[$slot[$i]]['id'];
if ($i < $dMax) {
echo "\t";
}
}
$maxVelocity = 0;
for ($i = 1; $i <= $dMax; $i++) {
$maxVelocity += $jobs[$slot[$i]]['velocity'];
}
echo "\nMax Velocity: " . $maxVelocity;
}
在这里,我们将获得作业列表(用户故事 ID、截止日期和速度),我们将使用这些作业来查找最大速度及其各自的用户故事 ID。首先,我们使用自定义用户排序函数usort对作业数组进行排序,并根据其速度按降序对数组进行排序。然后,我们计算 deadline 列中可用的最大插槽数。然后,我们将插槽数组初始化为-1,以保留已使用插槽的标志。下一个代码块是遍历每个用户故事,并为用户故事找到一个合适的槽。如果可用的时间段已满,我们将不再继续。现在,让我们使用以下代码块运行此代码:
$jobs = [
["id" => "S1", "deadline" => 2, "velocity" => 95],
["id" => "S2", "deadline" => 1, "velocity" => 32],
["id" => "S3", "deadline" => 2, "velocity" => 47],
["id" => "S4", "deadline" => 1, "velocity" => 42],
["id" => "S5", "deadline" => 3, "velocity" => 28],
["id" => "S6", "deadline" => 4, "velocity" => 64]
];
velocityMagnifier($jobs);
这将在命令行中生成以下输出:
Stories to Complete: S3 S1 S5 S6
Max Velocity: 234
贪婪算法有助于解决局部优化问题,如作业调度、网络流量控制、图算法等。然而,要获得全局优化的解决方案,我们需要关注算法的另一个方面,即动态规划。
动态规划是一种解决复杂问题的方法,它将复杂问题分解为更小的子问题,并为这些子问题寻找解决方案。我们积累子问题的解以找到全局解。动态规划的好处在于,我们通过存储子问题的结果来减少子问题的重新计算。动态规划是一种非常著名的优化方法。动态算法的使用在编程世界中随处可见。动态规划可以解决诸如换硬币、寻找最长公共子序列、寻找最长递增序列、对 DNA 字符串排序等问题。贪婪算法和动态规划之间的核心区别在于,动态规划总是喜欢全局优化的解决方案。
如果问题有最优子结构或重叠子问题,我们可以用动态规划来解决。最优子结构是指对实际问题的优化可以使用其子问题的最优解的组合来解决。换句话说,如果一个问题被优化为 n,它将被优化为任何小于 n 或大于 n 的大小。重叠子问题表明,较小的子问题将被反复解决,因为它们彼此重叠。斐波那契级数是重叠子问题的一个很好的例子。因此,在这里使用基本的递归将毫无帮助。动态规划只解决每个子问题一次,不试图进一步解决任何问题。它可以通过自上而下或自下而上的方法实现。
在自上而下的方法中,我们从一个较大的问题开始,递归地解决较小的子问题。然而,我们必须使用记忆技术来存储子问题结果,这样我们就不必在将来重新计算该子问题。在自底向上的方法中,我们首先解决最小的子问题,然后转移到其他较小的子问题。通常,子问题结果以表格格式存储,使用自下而上方法的多维数组。
现在,我们将探索动态编程世界中的一些示例。从我们日常的编程问题来看,有些可能听起来很熟悉。我们将从著名的背包问题开始。
背包是一种带肩带的袋子,通常由士兵携带,以帮助他们在旅途中携带必要的物品或贵重物品。每件物品都有一个价值和一定的重量。因此,士兵必须在最大重量限制内挑选最有价值的物品,因为他们不能将所有物品都放在包里。“0/1”这个词的意思是我们要么接受它,要么放弃它。我们不能部分接受一个项目。这就是著名的 0-1 背包问题。我们将采用自下而上的方法来解决 0-1 背包问题。以下是解决方案的伪代码:
Procedure knapsack(n, W, w1,...,wN, v1,...,vN)
for w = 0 to W
M[0, w] = 0
for i = 1 to n
for w = 0 to W
if wi > w :
M[i, w] = M[i-1, w]
else :
M[i, w] = max (M[i-1, w], vi + M[i-1, w-wi ])
return M[n, W]
end procedure
例如,如果我们有五个项目[1,2,3,4,5],它们的重量分别为 10,20,30,40,50,则允许的最大重量为 10 将使用自下而上的方法生成下表:
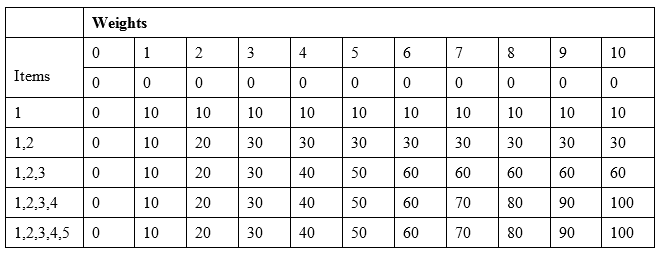
正如我们所看到的,我们从一个项目和一个权重开始,自下而上地构建表格,并将其增加到所需的权重,通过选择最好的项目使价值最大化。最后,右下角的最后一个单元格是 0-1 背包问题的预期结果。以下是运行该函数的实现和代码:
function knapSack(int $maxWeight, array $weights, array $values, int $n) {
$DP = [];
for ($i = 0; $i <= $n; $i++) {
for ($w = 0; $w <= $maxWeight; $w++) {
if ($i == 0 || $w == 0)
$DP[$i][$w] = 0;
else if ($weights[$i - 1] <= $w)
$DP[$i][$w] =
max($values[$i-1]+$DP[$i - 1][$w - $weights[$i-1]]
, $DP[$i - 1][$w]);
else
$DP[$i][$w] = $DP[$i - 1][$w];
}
}
return $DP[$n][$maxWeight];
}
$values = [10, 20, 30, 40, 50];
$weights = [1, 2, 3, 4, 5];
$maxWeight = 10;
$n = count($values);
echo knapSack($maxWeight, $weights, $values, $n);
这将在命令行上显示 100,这实际上与上表中的预期结果相匹配。该算法的复杂度为 O(*n**W,其中 n 为项数,W 为目标权重。
使用动态规划求解的另一个非常流行的算法是在两个字符串之间找到最长的公共子序列(LCS)。这个过程非常类似于背包解决方案,我们有一个二维表格,我们从一个重量开始移动到目标重量。在这里,我们将从第一个字符串的第一个字符开始,然后在整个字符串中移动第二个字符串以匹配这些字符。我们将继续此操作,直到第一个字符串的所有字符与第二个字符串的单个字符匹配为止。因此,当我们找到匹配时,我们考虑匹配单元的左上角单元或对角线左单元。让我们考虑下面两个表来理解匹配是如何发生的:
|
| | | A. | B | | | 0 | | | | 0】 | | | 【 | | 1。 |
|
| | | B | D | | 0 | | | | | | | | | | B | 0 | 1。 | 1。 | | D | 0 | 1。 | 2。 |
|
在左表中,我们有两个字符串 AB 和 CB。当 B 与表中的 B 匹配时,匹配单元格的值将是其对角线单元格的值加上一。这就是为什么第一个表格的黑色背景单元格的值为 1,因为对角左侧单元格的值为 0。出于同样的原因,右侧表格的右下单元格的值为 2,对角线单元格的值为 1。以下是用于查找 LCS 长度的伪代码:
function LCSLength(X[1..m], Y[1..n])
C = array[m][n]
for i := 0..m
C[i,0] = 0
for j := 0..n
C[0,j] = 0
for i := 1..m
for j := 1..n
if(i = 0 or j = 0)
C[i,j] := 0
else if X[i] = Y[j]
C[i,j] := C[i-1,j-1] + 1
else
C[i,j] := max(C[i,j-1], C[i-1,j])
return C[m,n]
以下是查找 LCS 长度的伪代码的实现:
function LCS(string $X, string $Y): int {
$M = strlen($X);
$N = strlen($Y);
$L = [];
for ($i = 0; $i <= $M; $i++)
$L[$i][0] = 0;
for ($j = 0; $j <= $N; $j++)
$L[0][$j] = 0;
for ($i = 0; $i <= $M; $i++) {
for ($j = 0; $j <= $N; $j++) {
if($i == 0 || $j == 0)
$L[$i][$j] = 0;
else if ($X[$i - 1] == $Y[$j - 1])
$L[$i][$j] = $L[$i - 1][$j - 1] + 1;
else
$L[$i][$j] = max($L[$i - 1][$j], $L[$i][$j - 1]);
}
}
return $L[$M][$N];
}
现在,让我们用两个字符串运行LCS函数,看看是否可以找到最长的公共子序列:
$X = "AGGTAB";
$Y = "GGTXAYB";
echo "LCS Length:".LCS( $X, $Y );
这将在命令行中生成输出LCS Length:5。这似乎是正确的,因为两个字符串都将 GGTAB 作为公共子序列。
我们刚刚看到了如何找到最长的公共子序列。利用同样的原理,我们可以实现 DNA 或蛋白质测序,这对我们解决生物信息学问题非常有帮助。为了对齐,我们将使用最流行的算法 Needleman-Wunsch 算法。它与我们的 LCS 算法相似,但评分系统不同。在这里,我们在不同的评分系统中为比赛、不匹配和差距评分。该算法分为两部分:一部分是用可能的序列计算矩阵,另一部分是用可能的最佳序列跟踪实际序列。Needleman-Wunsch 算法为任何给定序列提供最佳全局对齐解决方案。由于算法本身与评分系统的解释(我们可以在许多网站或书籍中找到)相比稍大一些,因此我们希望将重点放在算法的实现部分。我们将把这个问题分成两部分。首先,我们将使用动态规划生成计算表,然后,我们将向后跟踪它以生成实际的序列比对。对于我们的实现,我们将使用 1 表示匹配,使用-1 表示差距惩罚和不匹配分数。以下是我们实施的第一部分:
define("GC", "-");
define("SP", 1);
define("GP", -1);
define("MS", -1);
function NWSquencing(string $s1, string $s2) {
$grid = [];
$M = strlen($s1);
$N = strlen($s2);
for ($i = 0; $i <= $N; $i++) {
$grid[$i] = [];
for ($j = 0; $j <= $M; $j++) {
$grid[$i][$j] = null;
}
}
$grid[0][0] = 0;
for ($i = 1; $i <= $M; $i++) {
$grid[0][$i] = -1 * $i;
}
for ($i = 1; $i <= $N; $i++) {
$grid[$i][0] = -1 * $i;
}
for ($i = 1; $i <= $N; $i++) {
for ($j = 1; $j <= $M; $j++) {
$grid[$i][$j] = max(
$grid[$i - 1][$j - 1] + ($s2[$i - 1] === $s1[$j - 1] ? SP :
MS), $grid[$i - 1][$j] + GP, $grid[$i][$j - 1] + GP
);
}
}
printSequence($grid, $s1, $s2, $M, $N);
}
这里,我们创建了一个大小为 M,N 的二维数组,其中 M 是字符串#1 的大小,N 是字符串#2 的大小。我们将网格的第一行和第一列按降序初始化为负值。我们将指数与差距惩罚相乘以实现此行为。这里,我们的常量 SP 表示匹配分数点,MS 表示不匹配分数,GP 表示间隙惩罚,GC 表示间隙字符,我们将在序列打印期间使用。在动态规划结束时,将生成矩阵。让我们考虑以下两个字符串:
$X = "GAATTCAGTTA";
$Y = "GGATCGA";
然后,运行 Needleman 算法后,我们的表将如下所示:
| | | G | A. | A. | T | T | C | A. | G | T | T | A. | | | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | -10 | -11 | | G | -1 | 1. | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | | G | -2 | 0 | 0 | -1 | -2 | -3 | -4 | -5 | -4 | -5 | -6 | -7 | | A. | -3 | -1 | 1. | 1. | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -5 | | T | -4 | -2 | 0 | 0 | 2. | 1. | 0 | -1 | -2 | -3 | -4 | -5 | | C | -5 | -3 | -1 | -1 | 1. | 1. | 2. | 1. | 0 | -1 | -2 | -3 | | G | -6 | -4 | -2 | -2 | 0 | 0 | 1. | 1. | 2. | 1. | 0 | -1 | | A. | -7 | -5 | -3 | -1 | -1 | -1 | 0 | 2. | 1. | 1. | 0 | 1. |
现在,使用这个评分表,我们可以找出实际的顺序。这里,我们将从表中的右下角单元格开始,并考虑顶部单元格、左单元格和对角线单元格值。如果三个单元格中的最大值为顶部,则顶部字符串需要插入间隙字符(-)。如果最大值是对角值,则匹配的可能性更大。因此,我们可以比较两个字符串的两个字符,如果它们匹配,那么我们可以放置一个条形或管状字符来显示对齐方式。下面是排序函数的外观:
function printSequence($grid, $s1, $s2, $j, $i) {
$sq1 = [];
$sq2 = [];
$sq3 = [];
do {
$t = $grid[$i - 1][$j];
$d = $grid[$i - 1][$j - 1];
$l = $grid[$i][$j - 1];
$max = max($t, $d, $l);
switch ($max) {
case $d:
$j--;
$i--;
array_push($sq1, $s1[$j]);
array_push($sq2, $s2[$i]);
if ($s1[$j] == $s2[$i])
array_push($sq3, "|");
else
array_push($sq3, " ");
break;
case $t:
$i--;
array_push($sq1, GC);
array_push($sq2, $s2[$i]);
array_push($sq3, " ");
break;
case $l:
$j--;
array_push($sq1, $s1[$j]);
array_push($sq2, GC);
array_push($sq3, " ");
break;
}
} while ($i > 0 && $j > 0);
echo implode("", array_reverse($sq1)) . "\n";
echo implode("", array_reverse($sq3)) . "\n";
echo implode("", array_reverse($sq2)) . "\n";
}
因为我们从后面开始,慢慢地向前移动,所以我们使用阵列推力来保持对齐有序。然后,我们通过反转来打印阵列。该算法的复杂度为 O(M*N)。这是我们为两个字符串$X和$Y调用NWSquencing时的输出:
G-AATTCAGTTA
| | | | | |
GGA-T-C-G--A
回溯是一种递归算法策略,我们在没有找到结果时回溯,并以其他可能的方式继续搜索解决方案。回溯是解决许多著名问题的常用方法,尤其是国际象棋、数独、纵横字谜等。由于递归是回溯的关键组成部分,我们需要确保我们的问题可以划分为子问题,并且我们将递归应用到这些子问题中。在本节中,我们将使用回溯法解决最流行的游戏之一数独。
在数独游戏中,我们有一个部分填充的盒子,里面有 3X3 大小的漂亮盒子。游戏规则是在每个单元格中放置一个数字 1 到 9,同一行或列中不能存在相同的数字。因此,在 9X9 单元格中,每行和每列的每个数字 1 到 9 只出现一次:
| | | 7. | | 3. | | 8. | | | | | | | 2. | | 5. | | | | | 4. | | | 9 | | 6. | | | 1. | | | 4. | 3. | | | | 2. | 1. | | | 1. | | | | | | | | 5. | | | 5. | 8. | | | | 6. | 7. | | | 5. | | | 1. | | 8. | | | 9 | | | | | 5. | | 3. | | | | | | | 2. | | 9 | | 5. | | |
例如,在前面的数独板中,第一列有 4、1、5,第一行有 7、3、8。因此,我们不能在左上角的第一个空单元格中使用这六个数字中的任何一个。因此,可能的数字可以是 2、6 和 9。我们不知道这些数字中的哪一个会满足解决方案。我们可以选择两个并放入第一个单元格,然后开始查找剩余空单元格的值。这将一直持续到所有单元格都被填满,或者仍然可以在不违反游戏规则的情况下在空单元格中放置一个数字。如果没有可能的解决方案,我们将回溯并再次返回到 2,用下一个可能的选项 6 替换它,并运行相同的递归方法为其他空单元格查找数字。这将一直持续到董事会解决为止。让我们编写一些递归代码来解决数独问题:
define("N", 9);
define("UNASSIGNED", 0);
function FindUnassignedLocation(array &$grid, int &$row,
int &$col): bool {
for ($row = 0; $row < N; $row++)
for ($col = 0; $col < N; $col++)
if ($grid[$row][$col] == UNASSIGNED)
return true;
return false;
}
function UsedInRow(array &$grid, int $row, int $num): bool {
return in_array($num, $grid[$row]);
}
function UsedInColumn(array &$grid, int $col, int $num): bool {
return in_array($num, array_column($grid, $col));
}
function UsedInBox(array &$grid, int $boxStartRow,
int $boxStartCol, int $num): bool {
for ($row = 0; $row < 3; $row++)
for ($col = 0; $col < 3; $col++)
if ($grid[$row + $boxStartRow][$col + $boxStartCol] == $num)
return true;
return false;
}
function isSafe(array $grid, int $row, int $col, int $num): bool {
return !UsedInRow($grid, $row, $num) &&
!UsedInColumn($grid, $col, $num) &&
!UsedInBox($grid, $row - $row % 3, $col - $col % 3, $num);
}
在这里,我们可以看到实现Sudoku功能所需的所有辅助功能。首先,我们定义了网格的最大大小以及未分配的单元格指示符,在本例中为 0。我们拥有的第一个功能是从左上角单元格开始,在 9 X 9 网格中查找任何未分配的位置,并按行搜索空单元格。然后,我们有三个函数来检查数字是否用于特定的行、列或 3x3 框中。如果行、列或框中没有使用数字,我们可以将其用于单元格中的可能值,这就是为什么我们在isSafe函数检查中返回 true。如果在这些位置中的任何一个位置使用,该函数将返回 false。现在,我们已经准备好实现用于求解数独的递归函数:
function SolveSudoku(array &$grid): bool {
$row = $col = 0;
if (!FindUnassignedLocation($grid, $row, $col))
return true; // success! no empty space
for ($num = 1; $num <= N; $num++) {
if (isSafe($grid, $row, $col, $num)) {
$grid[$row][$col] = $num; // make assignment
if (SolveSudoku($grid))
return true; // return, if success
$grid[$row][$col] = UNASSIGNED; // failure
}
}
return false; // triggers backtracking
}
function printGrid(array $grid) {
foreach ($grid as $row) {
echo implode("", $row) . "\n";
}
}
SolveSudoku函数是不言自明的。在这里,我们访问了一个单元格,如果该单元格为空,则在单元格中放置一个临时数字,从 1 到 9 的任意数字。然后,我们检查行、列或 3 X 3 矩阵中的数字是否冗余。如果不冲突,我们将数字保留在单元格中,并移动到下一个空单元格。我们通过递归来实现这一点,这样,如果需要,我们可以在发生冲突的情况下跟踪并更改值。直到找到解决方案为止。我们还添加了一个printGrid函数,用于在命令行中打印给定的网格。现在让我们使用示例数独矩阵运行代码:
$grid = [
[0, 0, 7, 0, 3, 0, 8, 0, 0],
[0, 0, 0, 2, 0, 5, 0, 0, 0],
[4, 0, 0, 9, 0, 6, 0, 0, 1],
[0, 4, 3, 0, 0, 0, 2, 1, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 5],
[0, 5, 8, 0, 0, 0, 6, 7, 0],
[5, 0, 0, 1, 0, 8, 0, 0, 9],
[0, 0, 0, 5, 0, 3, 0, 0, 0],
[0, 0, 2, 0, 9, 0, 5, 0, 0]
];
if (SolveSudoku($grid) == true)
printGrid($grid);
else
echo "No solution exists";
我们使用了一个二维数组来表示数独矩阵。如果我们运行代码,它将在命令行中生成以下输出:
297431856
361285497
485976321
743659218
126847935
958312674
534128769
879563142
612794583
或者,如果我们在一个好的数独矩阵中展示,它将如下所示:
| 2. | 9 | 7. | 4. | 3. | 1. | 8. | 5. | 6. | | 3. | 6. | 1. | 2. | 8. | 5. | 4. | 9 | 7. | | 4. | 8. | 5. | 9 | 7. | 6. | 3. | 2. | 1. | | 7. | 4. | 3. | 6. | 5. | 9 | 2. | 1. | 8. | | 1. | 2. | 6. | 8. | 4. | 7. | 9 | 3. | 5. | | 9 | 5. | 8. | 3. | 1. | 2. | 6. | 7. | 4. | | 5. | 3. | 4. | 1. | 2. | 8. | 7. | 6. | 9 | | 8. | 7. | 9 | 5. | 6. | 3. | 1. | 4. | 2. | | 6. | 1. | 2. | 7. | 9 | 4. | 5. | 8. | 3. |
回溯对于寻找路径或解决游戏问题的解决方案非常有用。网上有很多回溯参考资料,对我们非常有用。
如今,推荐系统在互联网上随处可见。从电子商务网站到餐厅、酒店、门票、活动等等。在任何地方都推荐给我们。我们曾经问过自己,他们如何知道什么对我们最好?他们是如何计算出我们可能喜欢的物品的?答案是大多数网站使用协同过滤(CF)来推荐一些东西。协同过滤是通过分析其他用户的选择或偏好,对用户的兴趣进行自动预测(过滤)的过程(协同过滤)。我们将使用 Pearson 相关法构建一个简单的推荐系统,其中两个人之间的相似度得分计算范围为-1 到+1。如果相似度得分为+1,则表示两个人是完美的一对。如果相似性得分为 0,则表示它们之间不存在相似性,如果得分为-1,则表示它们具有负相似性。通常,分数都是分数。
皮尔逊相关性使用以下公式计算:
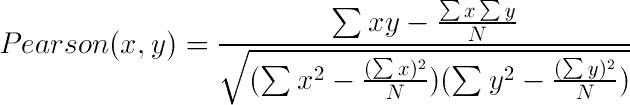
这里,x表示第一个人的偏好,y 表示第二个人的偏好,N 表示偏好中的项目数量,这在x和y之间是共同的。现在,让我们为达卡的餐厅实施一个示例审查系统。有些评论员对一些餐馆进行了评议。有些是常见的,有些不是。我们的工作是根据他人的评论为X人找到推荐信。我们的评论如下:
$reviews = [];
$reviews['Adiyan'] = ["McDonalds" => 5, "KFC" => 5, "Pizza Hut" => 4.5, "Burger King" => 4.7, "American Burger" => 3.5, "Pizza Roma" => 2.5];
$reviews['Mikhael'] = ["McDonalds" => 3, "KFC" => 4, "Pizza Hut" => 3.5, "Burger King" => 4, "American Burger" => 4, "Jafran" => 4];
$reviews['Zayeed'] = ["McDonalds" => 5, "KFC" => 4, "Pizza Hut" => 2.5, "Burger King" => 4.5, "American Burger" => 3.5, "Sbarro" => 2];
$reviews['Arush'] = ["KFC" => 4.5, "Pizza Hut" => 3, "Burger King" => 4, "American Burger" => 3, "Jafran" => 2.5, "FFC" => 3.5];
$reviews['Tajwar'] = ["Burger King" => 3, "American Burger" => 2, "KFC" => 2.5, "Pizza Hut" => 3, "Pizza Roma" => 2.5, "FFC" => 3];
$reviews['Aayan'] = [ "KFC" => 5, "Pizza Hut" => 4, "Pizza Roma" => 4.5, "FFC" => 4];
现在,基于这个结构,我们可以在两位评审员之间编写皮尔逊相关计算。以下是实施方案:
function pearsonScore(array $reviews, string $person1, string $person2): float {
$commonItems = array();
foreach ($reviews[$person1] as $restaurant1 => $rating) {
foreach ($reviews[$person2] as $restaurant2 => $rating) {
if ($restaurant1 == $restaurant2) {
$commonItems[$restaurant1] = 1;
}
}
}
$n = count($commonItems);
if ($n == 0)
return 0.0;
$sum1 = 0;
$sum2 = 0;
$sqrSum1 = 0;
$sqrSum2 = 0;
$pSum = 0;
foreach ($commonItems as $restaurant => $common) {
$sum1 += $reviews[$person1][$restaurant];
$sum2 += $reviews[$person2][$restaurant];
$sqrSum1 += $reviews[$person1][$restaurant] ** 2;
$sqrSum2 += $reviews[$person2][$restaurant] ** 2;
$pSum += $reviews[$person1][$restaurant] *
$reviews[$person2][$restaurant];
}
$num = $pSum - (($sum1 * $sum2) / $n);
$den = sqrt(($sqrSum1 - (($sum1 ** 2) / $n))
* ($sqrSum2 - (($sum2 ** 2) / $n)));
if ($den == 0) {
$pearsonCorrelation = 0;
} else {
$pearsonCorrelation = $num / $den;
}
return (float) $pearsonCorrelation;
}
这里,我们刚刚实现了皮尔逊相关计算器的等式。现在,我们将根据 Pearson 评分编写推荐函数:
function getRecommendations(array $reviews, string $person): array {
$calculation = [];
foreach ($reviews as $reviewer => $restaurants) {
$similarityScore = pearsonScore($reviews, $person, $reviewer);
if ($person == $reviewer || $similarityScore <= 0) {
continue;
}
foreach ($restaurants as $restaurant => $rating) {
if (!array_key_exists($restaurant, $reviews[$person])) {
if (!array_key_exists($restaurant, $calculation)) {
$calculation[$restaurant] = [];
$calculation[$restaurant]['Total'] = 0;
$calculation[$restaurant]['SimilarityTotal'] = 0;
}
$calculation[$restaurant]['Total'] += $similarityScore *
$rating;
$calculation[$restaurant]['SimilarityTotal'] +=
$similarityScore;
}
}
}
$recommendations = [];
foreach ($calculation as $restaurant => $values) {
$recommendations[$restaurant] = $calculation[$restaurant]['Total']
/ $calculation[$restaurant]['SimilarityTotal'];
}
arsort($recommendations);
return $recommendations;
}
在前面的函数中,我们计算了每个审阅者之间的相似性分数,并对他们的审阅进行加权。根据最高分,我们向评审员展示了推荐。让我们运行以下代码以获得一些建议:
$person = 'Arush';
echo 'Restaurant recommendations for ' . $person . "\n";
$recommendations = getRecommendations($reviews, $person);
foreach ($recommendations as $restaturant => $score) {
echo $restaturant . " \n";
}
这将产生以下输出:
Restaurant recommendations for Arush
McDonalds
Pizza Roma
Sbarro
我们可以使用 Pearson 相关性评分系统来推荐项目,或者向用户展示要跟随谁来获得更好的评论。还有许多其他方法可以让协同过滤发挥作用,但这超出了本书的范围。
稀疏矩阵可以作为一种高效的数据结构。与实际值相比,稀疏矩阵具有更多的 0 值。例如,100 X 100 矩阵可能有 10000 个单元。现在,在这 10000 个单元格中,只有 100 个有值;其余为 0。除了 100 个值之外,其余的单元格都被默认值 0 占用,并且它们采用相同的字节大小来存储值 0 以指示空单元格。这是一个巨大的空间浪费,我们可以使用稀疏矩阵来减少它。我们可以使用不同的技术将稀疏矩阵的值存储在一个单独的矩阵中,该矩阵非常精简,不会占用任何不必要的空间。我们也可以使用链表来表示稀疏矩阵。以下是稀疏矩阵的示例:
| 0
| 0 | 0 | 0 | 0 | 。 | 0 | 0 | 0 | 0 | | 1。 | 0 | 0 | 0 | 0 | | | | | | 【T | 0 | 0 | | 0 | 0 | 0 | | 2. | 0 | 0 | 0 | 0 | | | 0 | 2. | 0 | 0 | 0 | 0 | 0 | | 0 | 0 | | | | 0 | 0 | 1. | 0 | 【T204 0】 | | | 0 | 0 | 0 | 0 | 0 | 0 | 2. | 0 | 0 | | 0 | | 0 | 0 | 0 | 1. | 0 | | | | 1. | 0 | 0 | 0 | | 0 | 0 | 0 | 0 |
|
| 第 行 | Col | 值 | | 0 | 5。 | 1。 | | 1。 | 0 | 1。 | | 2。 | 4。 | 2。 | | 3。 | 2。 | 2。 | | 4。 | 6。 | 1。 | | 5。 | 7。 | 2。 | | 6。 | 6。 | 1。 | | 7。 | 1。 | 1。 |
|
由于 PHP 数组本质上是动态的,所以 PHP 中稀疏矩阵的最佳方法是只使用具有值的索引;其他的根本不用。当我们使用单元格时,我们可以检查单元格是否有任何值;否则,将使用默认值 0,如下例所示:
$sparseArray = [];
$sparseArray[0][5] = 1;
$sparseArray[1][0] = 1;
$sparseArray[2][4] = 2;
$sparseArray[3][2] = 2;
$sparseArray[4][6] = 1;
$sparseArray[5][7] = 2;
$sparseArray[6][6] = 1;
$sparseArray[7][1] = 1;
function getSparseValue(array $array, int $i, int $j): int {
if (isset($array[$i][$j]))
return $array[$i][$j];
else
return 0;
}
echo getSparseValue($sparseArray, 0, 2) . "\n";
echo getSparseValue($sparseArray, 7, 1) . "\n";
echo getSparseValue($sparseArray, 8, 8) . "\n";
这将在命令行中生成以下输出:
0
1
0
当我们有一个大的数据集时,在数据集中进行查找可能非常耗时和昂贵。假设我们有一个 1000 万个电话号码的数据集,并且我们想要搜索一个特定的电话号码。这可以使用数据库查询轻松完成。但是,如果是 10 亿个电话号码呢?从数据库中查找还会更快吗?如此大的数据库可能会造成执行缓慢的查找。为了解决这个问题,一种有效的方法是使用 bloom 过滤器。
bloom 筛选器是一种节省空间的概率数据结构,用于确定特定项是否为集合的一部分。它返回两个值:“可能在集合中”和“绝对不在集合中”。如果项目不属于集合,bloom filter 将返回 false。但是,如果返回 true,则该项可能在集合中,也可能不在集合中。这里描述了这样做的原因。
通常,bloom 过滤器是一个大小为 m 的位数组,其中所有初始值均为 0。有 k 个不同的hash函数,它将一个项转换为散列整数值,并映射到位数组中。这个散列值可以在 0 到 m 之间,因为 m 是位数组的最大大小。hash功能类似于md5、sha1、crc32等,但它们非常快速高效。通常,在 bloom 过滤器 fnv、杂音、Siphash 等中使用hash函数。让我们以初始值为 0 的 16(16+1 单元)位 bloom 过滤器为例:
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
假设我们有两个散列函数,k1和k2,用于将项目转换为 0 到 16 之间的整数值。让我们存储在 bloom 过滤器中的第一项为“PHP”。然后,我们的hash函数将返回以下内容:
k1("PHP") = 5
k2("PHP") = 9
两个hash函数返回了两个不同的值。现在我们可以在位数组中放入 1 来标记它。位数组现在将如下所示:
| 0 | 0 | 0 | 0 | 0 | 1. | 0 | 0 | 0 | 1. | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
现在让我们在列表中添加另一项,例如“算法”。假设我们的hash函数将返回以下值:
k1("algorithm") = 2
k2("algorithm") = 5
因为我们可以看到 5 已经被另一个项目标记,所以我们不必再次标记它。现在,位数组将如下所示:
| 0 | 0 | 1. | 0 | 0 | 1. | 0 | 0 | 0 | 1. | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
例如,现在我们要检查一个名为“error”的项,该项被散列为以下值:
k1("error") = 2
k2("error") = 9
我们可以看到,我们的hash函数k1和k2为字符串“error”返回了一个散列值,该值在数组中不存在。所以,这肯定是一个错误,如果我们的hash函数数量很少,我们预计会出现这样的错误。我们拥有的hash函数越多,错误就越小,因为不同的hash函数将返回不同的值。错误率、hash函数的数量和 bloom 过滤器的大小之间存在关系。例如,用于 5000 项和 0.0001 错误率的 bloom 过滤器将需要大约 14 个hash功能和大约 96000 位。我们可以从在线 bloomfilter 计算器(如)中获得这些数字 https://krisives.github.io/bloom-calculator/ 。
在本章中,我们已经看到了许多可以用来解决不同类型问题的高级算法和技术。有许多很好的资源可用于研究这些主题。动态规划是一个非常重要的主题,可以在几章中介绍,也可以单独编写一本书。我们试图解释的主题很少,但还有更多的探索。您还了解了稀疏矩阵和 bloom 过滤器,它们可用于大数据块的高效数据存储。我们可以随时使用这些数据结构概念。现在,随着本书的结束,我们将用 PHP7 中数据结构和算法的一些可用库、函数和参考来结束我们的讨论。
 PDF电子书集合
PDF电子书集合