- PHP7 数据结构和算法

PHP 理解和实现树详解
到目前为止,我们对数据结构的探索只涉及线性部分。无论我们使用数组、链表、栈还是队列,都是线性数据结构。我们已经看到了线性数据结构操作的复杂性,大多数情况下,插入和删除都可以以O(1)复杂度执行。但是,搜索有点复杂,需要O(n)复杂度。唯一的例外是 PHP 数组,它实际上是一个哈希表,如果以这种方式管理索引或键,则可以在O(1)中进行搜索。为了解决这个问题,我们可以使用分层数据结构来代替线性数据结构。分层数据可以解决线性数据结构无法轻松解决的许多问题。每当我们谈论家谱图、组织结构图和网络连接图时,实际上我们谈论的是分层数据。树是表示层次数据的一种特殊的抽象数据类型(ADT。与链表不同,链表也是 ADT,与链表的线性性质相比,树是分层的。在本章中,我们将探索树木的世界。树结构的完美示例可以是家谱,如下图所示:
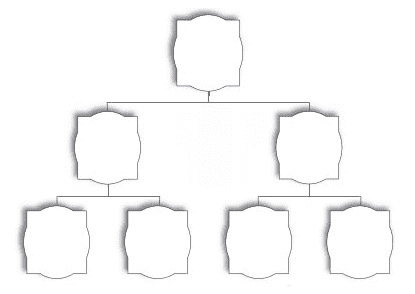
树是由边连接的节点或顶点的分层集合。树不能有循环,并且节点与其下一个节点或子节点之间只存在边。同一父节点的两个子节点之间不能有任何边。每个节点都可以有除顶部节点(也称为根节点)之外的父节点。每个树只能有一个根节点。每个节点可以有零个或多个子节点。下图中,A为根节点,B、C、D为A的子节点。也可以说 A 是B、C和D的父节点。B、C和D被称为兄弟节点,因为它们是来自同一父节点的子节点,A:
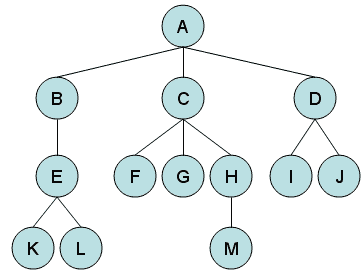
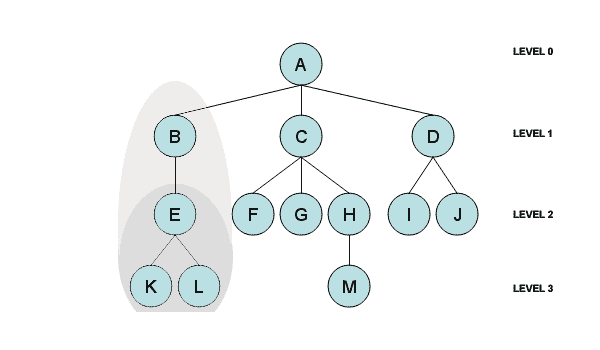
没有任何子节点的节点称为叶节点。在上图中,K、L、F、G、M、I和J为叶节点。叶节点也称为外部节点或终端节点。除根节点外,具有至少一个子节点的节点称为内部节点。这里,B、C、D、E和H是内部节点。下面是我们在描述树数据结构时使用的一些其他常用术语:
-
节点高度:节点高度由节点与下一节点最深层之间的边数定义。例如,节点B的高度为 2。
-
级别:该级别代表节点的生成。如果父节点处于n级别,则其子节点将处于n+1级别。因此,级别由节点和根之间的 1+边数定义。在这里:
-
树的高度:树的高度由其根节点的高度定义。在这里,树的高度是 3。
-
子树:在树结构中,每个子树递归形成一个子树。换句话说,一棵树由许多子树组成。例如,B与E、K和L构成子树,E与K和L构成子树。在前面的示例中,我们在左侧以不同的阴影标识了每个。我们也可以对C和D及其子树执行相同的操作。
-
深度:节点的深度由节点与根节点之间的边数决定。例如,在我们的树图像中,H的深度是 2,L的深度是 3。
-
森林:森林是一组零棵或多棵不相交的树。
-
遍历:表示按特定顺序访问节点的过程。我们将在接下来的章节中经常使用这个术语。
-
键:键是节点中用于搜索目的的值。
到目前为止,您已经了解了树数据结构的不同属性。如果我们将树数据结构与真实的例子进行比较,我们可以考虑我们的组织结构或家族树来表示数据结构。对于组织结构,有一个根节点可以是公司的 CEO,然后是 CXO 级别的员工,然后是其他级别的员工。这里,我们不限制特定节点的任何程度。这意味着一个节点可以有多个子节点。那么,让我们考虑一个节点结构,我们可以在其中定义节点属性、其父节点及其子节点。它可能看起来像这样:
class TreeNode {
public $data = NULL;
public $children = [];
public function __construct(string $data = NULL) {
$this->data = $data;
}
public function addChildren(TreeNode $node) {
$this->children[] = $node;
}
}
如果我们查看前面的代码,我们可以看到我们已经为数据和子项声明了两个公共属性。我们还提供了一种将子节点添加到特定节点的方法。这里,我们只是将新的子节点附加到数组的末尾。这将为我们提供一个选项,可以将多个节点添加为特定节点的子节点。由于树是一种递归结构,它将帮助我们递归地构建树,并以递归的方式遍历树。
现在,我们有了节点;让我们构建一个树结构,它将定义树的根节点以及遍历整个树的方法。因此,基本树结构如下所示:
class Tree {
public $root = NULL;
public function __construct(TreeNode $node) {
$this->root = $node;
}
public function traverse(TreeNode $node, int $level = 0) {
if ($node) {
echo str_repeat("-", $level);
echo $node->data . "\n";
foreach ($node->children as $childNode) {
$this->traverse($childNode, $level + 1);
}
}
}
}
前面的代码显示了一个简单的树类,我们可以在其中存储根节点引用,也可以从任何节点遍历树。在遍历部分,我们访问每个子节点,然后立即递归调用遍历方法以获取当前节点的子节点。我们正在传递一个级别,以便在节点名称的开头打印一个破折号(-),以便我们能够轻松地理解子级别的数据。
现在,让我们创建根节点并将其作为根节点分配给树。代码如下所示:
$ceo = new TreeNode("CEO");
$tree = new Tree($ceo);
在这里,我们创建了第一个节点作为 CEO,然后创建了树,并将 CEO 节点指定为树的根节点。现在,是时候从根节点开始生长我们的树了。由于我们选择了 CEO 的例子,现在我们将在 CEO 下面添加 CXO 和其他员工。以下是此操作的代码:
$cto = new TreeNode("CTO");
$cfo = new TreeNode("CFO");
$cmo = new TreeNode("CMO");
$coo = new TreeNode("COO");
$ceo->addChildren($cto);
$ceo->addChildren($cfo);
$ceo->addChildren($cmo);
$ceo->addChildren($coo);
$seniorArchitect = new TreeNode("Senior Architect");
$softwareEngineer = new TreeNode("Software Engineer");
$userInterfaceDesigner = new TreeNode("User Interface Designer");
$qualityAssuranceEngineer = new TreeNode("Quality Assurance Engineer");
$cto->addChildren($seniorArchitect);
$seniorArchitect->addChildren($softwareEngineer);
$cto->addChildren($qualityAssuranceEngineer);
$cto->addChildren($userInterfaceDesigner);
$tree->traverse($tree->root);
在这里,我们首先创建四个新节点(CTO、CFO、CMO 和 COO),并将它们分配为 CEO 节点的子节点。然后我们创建高级架构师,这里是软件工程师节点,后面是用户界面设计师和质量保证工程师。我们已指定高级软件工程师节点为高级架构师节点的子节点,高级架构师节点为 CTO 的子节点,以及用户界面工程师和质量保证工程师。最后一行显示从根开始的树。这将在命令行中输出以下行:
CEO
-CTO
--Senior Architect
---Software Engineer
--Quality Assurance Engineer
--User Interface Designer
-CFO
-CMO
-COO
如果我们考虑前面的输出,我们在 0 级上有 0。CTO、CFO、CMO、COO为一级。Senior Architect、User Interface Designer、Quality Assurance Engineer为二级;Software Engineer为三级。
我们使用 PHP 构建了一个基本的树数据结构。现在,我们将探索我们拥有的不同类型的树。
编程世界中存在许多类型的树数据结构。我们将在这里探索一些最常用的树结构。
二进制是树结构的最基本形式,其中每个节点最多有两个子节点。子节点称为左节点和右节点。二叉树将如下图所示:
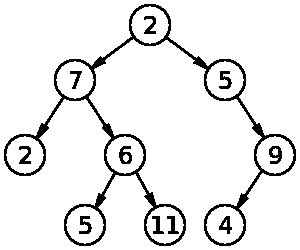
二叉搜索树(BST)是一种特殊类型的二叉树,其中节点以排序方式存储。它的排序方式是,在任何给定点,节点值必须大于或等于左子节点值,小于右子节点值。每个节点都必须满足这个属性,将其视为二进制搜索树。由于节点是按特定顺序排序的,因此二进制搜索算法可以应用于在对数时间内搜索 BST 中的项目。它总是比线性搜索要好,线性搜索需要O(n)时间,我们将在下一章中对此进行探讨。以下是二进制搜索树的示例:
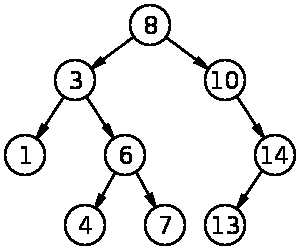
自平衡二叉搜索树或高度平衡二叉搜索树是一种特殊类型的二叉搜索树,它试图通过自动调整使树的高度或层次数尽可能小。例如,下图显示了左侧的二元搜索树和右侧的自平衡二元搜索树:
与常规 BST 相比,高度平衡二叉树总是更好,因为它有助于更快地执行搜索操作。自平衡或高度平衡二叉搜索树有不同的实现。以下是一些受欢迎的方案:
- AA 树
- 平衡二叉树
- 红黑树
- 替罪羊树
- 八字树
- 2-3 棵树
- 树堆
我们将在以下章节中讨论几个高度平衡的树。
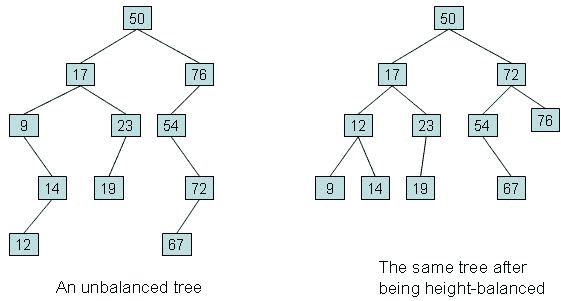
AVL 树是一种自平衡二叉搜索树,其中一个节点的两个子树的高度最大相差 1。如果高度增加,在任何情况下,都将进行重新平衡,使高度差为 1。这为 AVL 树增加了对数复杂度的优势,可用于不同的操作。以下是 AVL 树的示例:
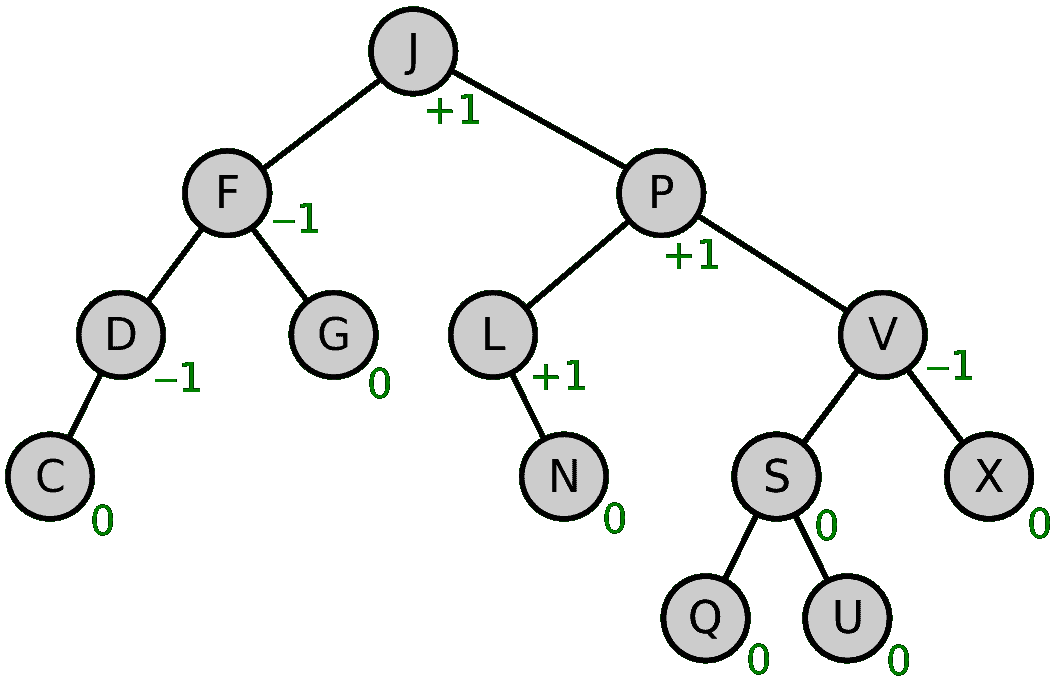
红黑树是一种自平衡二叉搜索树,具有一些额外的属性,即颜色。二叉树中的每个节点存储一个额外的信息位,称为颜色,可以使用红色或黑色作为值。与 AVL 树一样,红黑树也用于实时应用程序,因为平均和最坏情况复杂性也是对数的。红黑树示例如下所示:
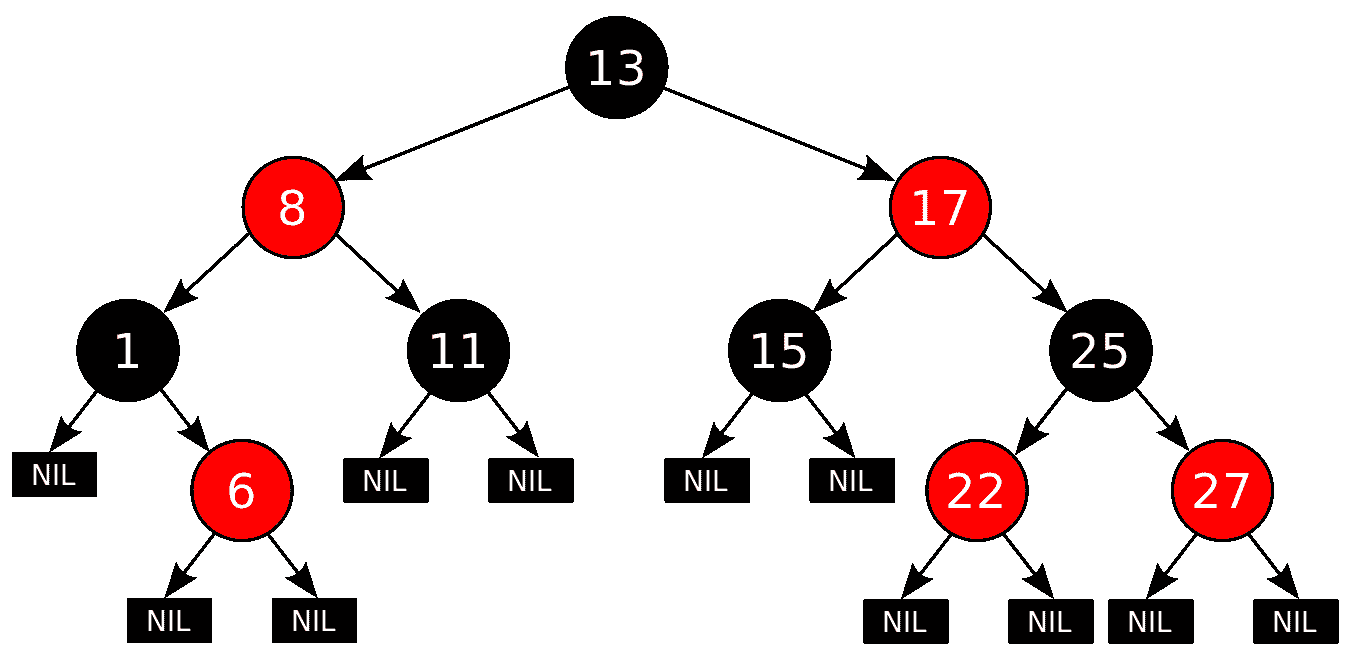
B-树是一种特殊类型的二叉树,它是自平衡的。这与自平衡二叉搜索树不同。关键的区别在于,在 B-树中,我们可以有任意数量的节点作为子节点,而不仅仅是两个。B 树用于大量数据,主要用于文件系统和数据库。B-树中不同操作的复杂性是对数的。
N 元树是一种特殊类型的树,其中一个节点最多可以有 N 个子节点。这也称为 k-way 树或 M-ary 树。二叉树是 N 元树,其中 N 的值为 2。
我们总是混淆二叉树和二叉搜索树。正如我们在定义中看到的,BST 是一个排序的二叉树。如果对其进行排序,那么与常规二叉树相比,我们可以获得性能改进。每个二叉树节点最多可以有两个子节点,即左子节点和右子节点。但是,根据二叉树的类型,可以有零个、一个或两个子节点。
我们还可以将二叉树分为不同的类别:
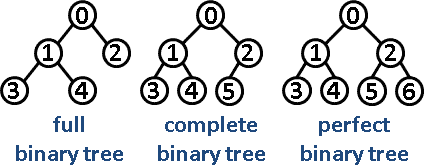
- 全二叉树:全二叉树是指每个节点上有零个或两个子节点的树。完整二叉树也称为真树或平面二叉树。
- 完美二叉树:完美二叉树是一种二叉树,其中所有内部节点正好有两个子节点,所有叶子具有相同的层次或深度。
- 完全二叉树:完全二叉树是一种二叉树,其中除最后一级外的所有级别都被完全填充,并且所有节点都尽可能向左。下图显示了完整二叉树、完整二叉树和完美二叉树:
现在我们将创建一个二叉树(不是二叉搜索树)。二叉树中的关键因素是,必须为左子节点和右子节点提供两个占位符,以及要存储在节点中的数据。二进制节点的简单实现如下所示:
class BinaryNode {
public $data;
public $left;
public $right;
public function __construct(string $data = NULL) {
$this->data = $data;
$this->left = NULL;
$this->right = NULL;
}
public function addChildren(BinaryNode $left, BinaryNode $right) {
$this->left = $left;
$this->right = $right;
}
}
前面的代码显示,我们有一个具有树属性的类来存储左右数据。当我们构建一个新节点时,我们将节点值添加到数据属性中,并保留左侧和右侧NULL,因为我们不确定是否需要它们。我们还有一个addChildren方法将左子节点和右子节点添加到特定节点。
现在,我们将创建一个二叉树类,在这里我们可以定义根节点以及遍历方法,类似于本章前面的基本树实现。两种实现之间的区别在于遍历过程。在前面的示例中,我们使用foreach遍历每个子节点,因为我们不知道有多少节点。由于二叉树中的每个节点最多可以有两个节点,它们被命名为 left 和 right,因此对于每个特定的节点访问,我们只能遍历 left 节点,然后遍历 right 节点。更改后的代码如下所示:
class BinaryTree {
public $root = NULL;
public function __construct(BinaryNode $node) {
$this->root = $node;
}
public function traverse(BinaryNode $node, int $level
= 0) {
if ($node) {
echo str_repeat("-", $level);
echo $node->data . "\n";
if ($node->left)
$this->traverse($node->left, $level + 1);
if ($node->right)
$this->traverse($node->right, $level + 1);
}
}
}
它看起来与本章前面的基本树类非常相似。现在,让我们用一些节点填充二叉树。通常,在任何足球或板球比赛中,我们都会有淘汰赛,两队相互比赛,胜者向前移动,直到决赛。对于我们的示例,我们可以使用与二叉树相似的结构。因此,让我们创建一些二进制节点,并将它们组织成一个层次结构:
$final = new BinaryNode("Final");
$tree = new BinaryTree($final);
$semiFinal1 = new BinaryNode("Semi Final 1");
$semiFinal2 = new BinaryNode("Semi Final 2");
$quarterFinal1 = new BinaryNode("Quarter Final 1");
$quarterFinal2 = new BinaryNode("Quarter Final 2");
$quarterFinal3 = new BinaryNode("Quarter Final 3");
$quarterFinal4 = new BinaryNode("Quarter Final 4");
$semiFinal1->addChildren($quarterFinal1, $quarterFinal2);
$semiFinal2->addChildren($quarterFinal3, $quarterFinal4);
$final->addChildren($semiFinal1, $semiFinal2);
$tree->traverse($tree->root);
首先,我们创建了一个名为 final 的节点,并将其作为根节点。然后,我们创建了两个半决赛节点和四个四分之一决赛节点。两个半决赛节点各自有两个四分之一决赛节点作为左和右子节点。最终节点有两个半最终节点作为左和右子节点。addChildren方法是为节点做子节点分配工作。在最后一行中,我们遍历了树并按层次显示了数据。如果在命令行中运行此代码,我们将看到以下输出:
Final
-Semi Final 1
--Quarter Final 1
--Quarter Final 2
-Semi Final 2
--Quarter Final 3
--Quarter Final 4
我们可以使用 PHP 数组实现二叉树。由于二叉树的最大子节点数为 0 到 2,因此我们可以将最大子节点数用作 2,并构造一个公式来查找给定节点的子节点。让我们对二叉树中的节点从上到下、从左到右进行编号。因此,根节点将有编号0、左子节点1和右子节点2,这将一直持续到每个节点编号为止,如下图所示:
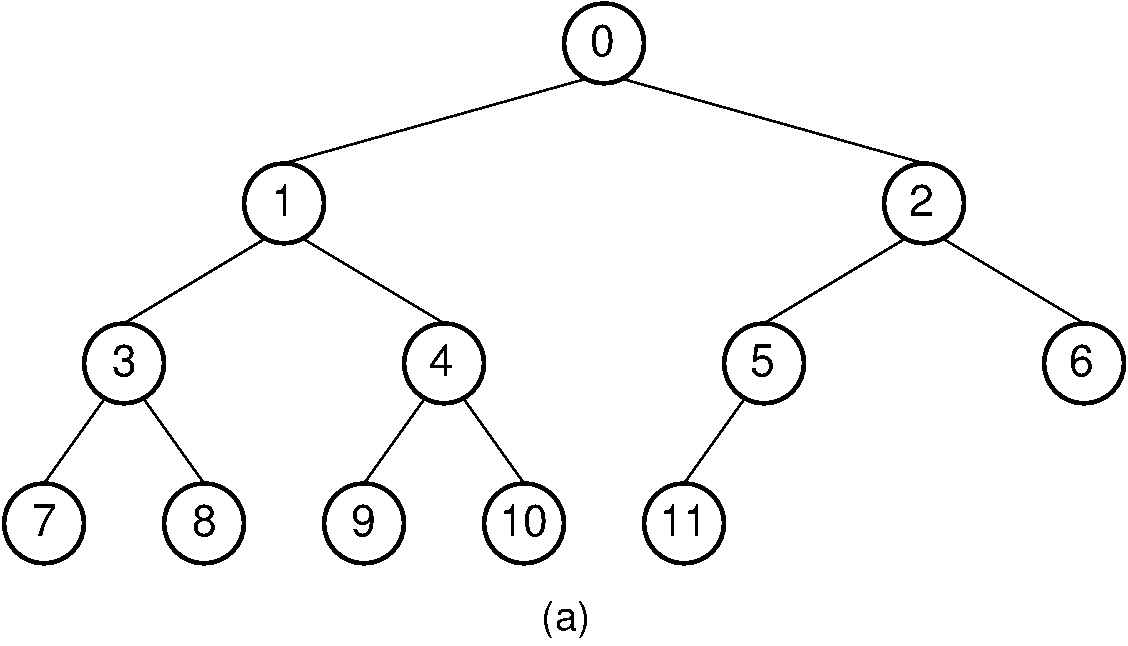
我们可以很容易地看到,对于节点0,左边的子节点是1、,右边的子节点是2。对于节点1,左边的子节点是3、,右边的子节点是4,并且继续。我们可以很容易地将其放入公式中:
如果i是我们的节点号,那么:
左节点=2xi+1
右节点=2x(i+1)
现在让我们使用 PHP 数组为 match schedule 部分创建示例。如果我们根据我们的讨论对其进行排序,则其将如下所示:
$nodes = [];
$nodes[] = "Final";
$nodes[] = "Semi Final 1";
$nodes[] = "Semi Final 2";
$nodes[] = "Quarter Final 1";
$nodes[] = "Quarter Final 2";
$nodes[] = "Quarter Final 3";
$nodes[] = "Quarter Final 4";
基本上,我们将创建一个具有自动索引的数组,从 0 开始。此数组将用作二叉树表示形式。现在,我们将修改我们的BinaryTree类以使用这个数组而不是我们的节点类,使用左、右子节点以及遍历方法。现在,我们将根据节点编号而不是实际节点参考进行遍历:
class BinaryTree {
public $nodes = [];
public function __construct(Array $nodes) {
$this->nodes = $nodes;
}
public function traverse(int $num = 0, int $level = 0) {
if (isset($this->nodes[$num])) {
echo str_repeat("-", $level);
echo $this->nodes[$num] . "\n";
$this->traverse(2 * $num + 1, $level+1);
$this->traverse(2 * ($num + 1), $level+1);
}
}
}
从前面的实现中我们可以看到,遍历部分使用节点定位而不是引用。这个节点位置只是数组索引。因此,我们可以直接访问数组索引并检查它是否为空。如果没有,我们可以使用递归方法继续深入。如果要使用数组创建二叉树并打印数组值,则必须编写以下代码:
$tree = new BinaryTree($nodes);
$tree->traverse(0);
如果在命令行中运行此代码,我们将看到以下输出:
Final
-Semi Final 1
--Quarter Final 1
--Quarter Final 2
-Semi Final 2
--Quarter Final 3
--Quarter Final 4
We can use a simple while loop to iterate through the array and visit each node instead of proceeding recursively. In all our recursive examples, we will see that some are more efficient if we use them the iterative way. We can also just use them directly instead of creating a class for the binary tree.
BST 是一个二叉树,它的构建方式使树始终被排序。这意味着左侧子节点的值小于或等于父节点值,右侧子节点的值将大于父节点值。所以,每当我们需要搜索一个值时,我们要么向左搜索,要么向右搜索。当它被排序时,我们必须搜索树的一部分,而不是两部分,这将递归地继续。由于它的可分性,搜索变得非常快,我们可以实现对数复杂度的搜索。例如,如果我们有n个节点,我们将搜索前半部分或后半部分节点。一旦我们进入了上半部分或下半部分,我们可以将它再次分成两半,这意味着我们的一半现在变成了四分之一,它会一直持续下去,直到我们到达最后一个节点。由于我们不会移动到每个节点进行搜索,因此操作不会花费O(n)复杂性。在下一章中,我们将对二元搜索进行复杂性分析,并将了解为什么二元搜索树的搜索复杂性为O(log n)。与二叉树不同,我们不能在不重建 BST 属性的情况下向树中添加任何节点或从树中删除任何节点。
如果节点X有两个子节点,则节点X的后继节点是属于树的最小值,大于X的值。换句话说,后继者是右子树的最小值。另一方面,前置是左子树的最大值。现在,我们将更多关注 BST 的不同操作以及我们需要考虑的步骤来正确地执行这些操作。
以下是 BST 的操作。
当我们在二进制搜索树中插入一个新的节点时,我们必须考虑以下步骤:
- 将新节点创建为叶(无左子节点或右子节点)。
- 从根节点开始,并将其设置为当前节点。
- 如果节点为空,则将新节点作为根节点。
- 检查新值是小于当前节点还是大于当前节点。
- 如果较少,请转到左侧,并将左侧设置为当前节点。
- 如果更多,请转到右侧并将右侧设置为当前节点。
- 继续步骤 3直到访问了所有节点并设置了新节点。
当我们在二叉搜索树中搜索一个新的节点时,我们必须考虑以下步骤:
- 从根节点开始,并将其设置为当前节点。
- 如果当前节点为空,则返回 false。
- 如果当前节点值是搜索值,则返回 true。
- 检查搜索值是否小于或大于当前节点。
- 如果较少,请转到左侧,并将左侧设置为当前节点。
- 如果更多,请转到右侧并将右侧设置为当前节点。
- 继续步骤 3直到访问所有节点。
由于二叉搜索树以排序的方式存储数据,我们总是可以在左侧节点中找到较小的数据,在右侧节点中找到较大的数据。因此,找到最小值需要我们从根节点访问所有左侧节点,直到找到最左侧的节点及其值。以下是查找最小值的步骤:
- 从根节点开始,并将其设置为当前节点。
- 如果当前节点为空,则返回 false。
- 转到左侧并将左侧设置为当前节点。
- 如果当前节点没有左节点,则进入步骤 5;否则,继续执行步骤 4。
- 继续步骤 3直到访问所有左侧节点。
- 返回当前节点。
以下是查找最大值的步骤:
- 从根节点开始,并将其设置为当前节点。
- 如果当前节点为空,则返回 false。
- 转到右侧并将右侧设置为当前节点。
- 如果当前节点没有右节点,则进入步骤 5;否则,继续执行步骤 4。
- 继续步骤 3直到访问了所有正确的节点。
- 返回当前节点。
当我们删除一个节点时,我们必须考虑节点可以是内部节点或叶。如果它是一片叶子,它就没有孩子。但是,如果节点是内部的,则它可以有一个或两个子节点。在这种情况下,我们需要采取额外的步骤来确保在删除之后立即构建树。这就是为什么与其他操作相比,从 BST 中删除节点始终是一项具有挑战性的工作。以下是节点删除时需要考虑的事项:
- 如果节点没有子节点,则将节点设为 NULL。
- 如果节点只有一个子节点,则将该子节点替换为节点。
- 如果节点有两个子节点,则找到节点的后续节点并将其替换到当前节点的位置。删除后续节点。
我们已经讨论了二进制搜索树的大多数可能操作。现在,我们将逐步实现二进制搜索树,从插入、搜索、查找最小值和最大值开始,最后执行删除操作。让我们从实现开始。
正如我们所知,一个节点可以有两个子节点,并且节点本身可以以递归的方式表示一棵树。我们将把我们的节点类定义为更具功能性,并具有查找最大值、最小值、前置值和后续值所需的所有功能。稍后,我们还将为节点添加删除功能。让我们检查 BST 节点类的以下代码:
class Node {
public $data;
public $left;
public $right;
public function __construct(int $data = NULL) {
$this->data = $data;
$this->left = NULL;
$this->right = NULL;
}
public function min() {
$node = $this;
while($node->left) {
$node = $node->left;
}
return $node;
}
public function max() {
$node = $this;
while($node->right) {
$node = $node->right;
}
return $node;
}
public function successor() {
$node = $this;
if($node->right)
return $node->right->min();
else
return NULL;
}
public function predecessor() {
$node = $this;
if($node->left)
return $node->left->max();
else
return NULL;
}
}
node 类看起来很简单,并且与上一节中定义的步骤相匹配。每个新节点都是一个叶,因此在创建时没有左或右节点。正如我们所知,我们可以在节点左侧找到较小的值以找到最小值,我们正在到达最左侧节点和最右侧节点以获得最大值。对于后继部分,我们从给定节点的右子树中查找节点的最小值,从前导部分的左子树中查找节点的最大值。
现在,我们需要一个 BST 结构来在树中添加新节点,以便我们可以遵循插入原则:
class BST {
public $root = NULL;
public function __construct(int $data) {
$this->root = new Node($data);
}
public function isEmpty(): bool {
return $this->root === NULL;
}
public function insert(int $data) {
if($this->isEmpty()) {
$node = new Node($data);
$this->root = $node;
return $node;
}
$node = $this->root;
while($node) {
if($data > $node->data) {
if($node->right) {
$node = $node->right;
} else {
$node->right = new Node($data);
$node = $node->right;
break;
}
} elseif($data < $node->data) {
if($node->left) {
$node = $node->left;
} else {
$node->left = new Node($data);
$node = $node->left;
break;
}
} else {
break;
}
}
return $node;
}
public function traverse(Node $node) {
if ($node) {
if ($node->left)
$this->traverse($node->left);
echo $node->data . "\n";
if ($node->right)
$this->traverse($node->right);
}
}
}
如果我们查看前面的代码,那么 BST 类只有一个属性,它将标记根节点。在构建 BST 对象的过程中,我们传递一个值,该值将用作树的根。isEmpty方法检查树是否为空。insert方法允许我们在树中添加一个新节点。该逻辑检查该值是否大于或小于根节点,并遵循 BST 的原则将新节点插入正确的位置。如果该值已经插入,我们将忽略它并避免添加到树中。
我们还有一个traverse方法来遍历节点,并以有序的格式查看数据(首先是左节点,然后是节点,然后是右节点值)。它有一个指定的名称,我们将在下一节中对此进行探讨。现在,让我们准备一个使用 BST 类的示例代码,添加一些数字,并检查这些数字是否以正确的方式存储。如果 BST 正在工作,则遍历将显示一个已排序的数字列表,无论我们如何插入它们:
$tree = new BST(10);
$tree->insert(12);
$tree->insert(6);
$tree->insert(3);
$tree->insert(8);
$tree->insert(15);
$tree->insert(13);
$tree->insert(36);
$tree->traverse($tree->root);
如果我们看前面的代码,10是我们的根节点,然后,我们随机添加了新节点。最后,我们调用了遍历方法来显示节点以及它们如何存储在二叉搜索树中。以下是前面代码的输出:
3
6
8
10
12
13
15
36
实际的树在视觉上看起来像这样,与 BST 实现的预期完全相同:
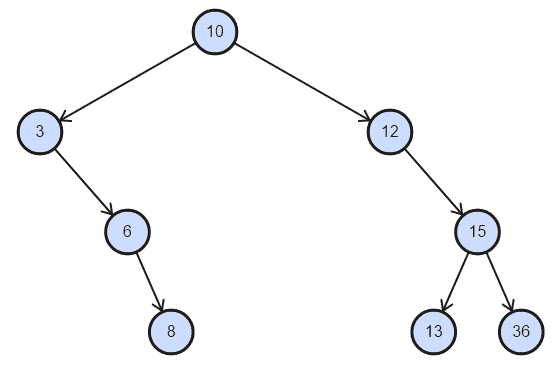
现在,我们将在 BST 类中添加搜索部分。我们想知道这个值是否存在于树中。如果该值不在我们的 BST 中,它将返回 false,而节点返回 false。以下是简单的搜索功能:
public function search(int $data) {
if ($this->isEmpty()) {
return FALSE;
}
$node = $this->root;
while ($node) {
if ($data > $node->data) {
$node = $node->right;
} elseif ($data < $node->data) {
$node = $node->left;
} else {
break;
}
}
return $node;
}
在前面的代码中,我们可以看到我们正在从节点搜索树中的一个值,并迭代地跟随树的左侧或右侧。如果没有找到该值的节点,则返回该节点的叶子,即NULL.我们可以这样测试代码:
echo $tree->search(14) ? "Found" : "Not Found";
echo "\n";
echo $tree->search(36) ? "Found" : "Not Found";
这将产生以下输出。由于14不在我们的列表中,它将显示Not Found,对于36,它将显示Found:
Not Found
Found
现在,我们将转到编码中最复杂的部分,删除节点。我们需要实现每个节点可以有零、一或两个子节点的情况。下图向我们展示了删除节点并确保二叉搜索树在操作后保持为二叉搜索树所需满足的三个条件。在处理具有两个子节点的节点时,我们必须小心。因为我们需要在节点之间来回移动,所以我们需要知道哪个节点是当前节点的父节点。因此,我们需要添加一个附加属性来跟踪任何节点的父节点:
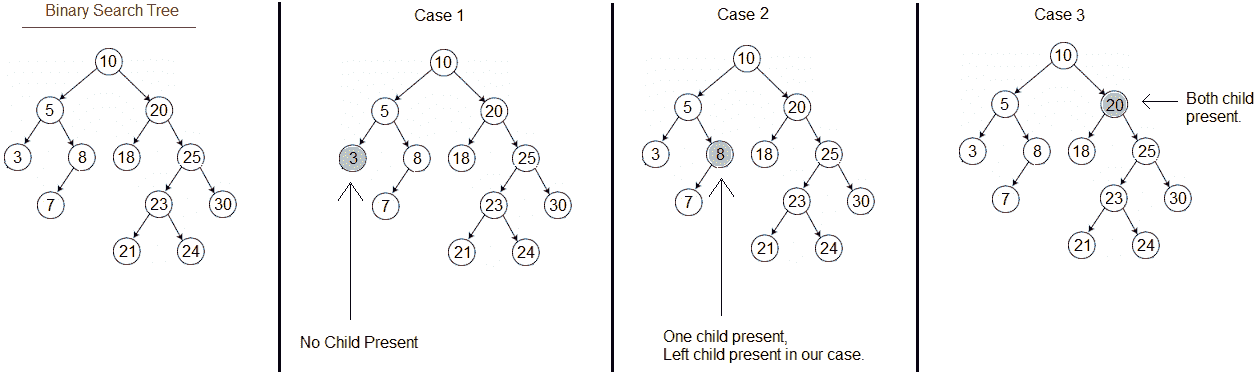
下面是我们在Node类中添加的代码更改:
public $data;
public $left;
public $right;
public $parent;
public function __construct(int $data = NULL, Node $parent = NULL)
{
$this->data = $data;
$this->parent = $parent;
$this->left = NULL;
$this->right = NULL;
}
这个代码块现在还创建了一个与新创建的节点及其直接父节点的父关系。我们还希望将删除功能附加到单个节点上,这样我们就可以找到一个节点,然后使用delete方法将其删除。以下是删除功能的代码:
public function delete() {
$node = $this;
if (!$node->left && !$node->right) {
if ($node->parent->left === $node) {
$node->parent->left = NULL;
} else {
$node->parent->right = NULL;
}
} elseif ($node->left && $node->right) {
$successor = $node->successor();
$node->data = $successor->data;
$successor->delete();
} elseif ($node->left) {
if ($node->parent->left === $node) {
$node->parent->left = $node->left;
$node->left->parent = $node->parent->left;
} else {
$node->parent->right = $node->left;
$node->left->parent = $node->parent->right;
}
$node->left = NULL;
} elseif ($node->right) {
if ($node->parent->left === $node) {
$node->parent->left = $node->right;
$node->right->parent = $node->parent->left;
} else {
$node->parent->right = $node->right;
$node->right->parent = $node->parent->right;
}
$node->right = NULL;
}
}
第一个条件检查节点是否为叶。如果节点是一个叶子,那么我们只是让父节点删除子节点的引用(左或右)。这样,节点将与树断开连接,这满足了我们的第一个条件,即没有子节点。
下一个条件实际上检查我们的第三个条件,其中我们有一个节点的两个子节点。在这种情况下,我们将获取节点的后继节点,将后继节点值分配给节点本身,并删除后继节点。它只是来自后继数据的复制粘贴。
接下来的两个条件检查节点是否有一个子节点,如前面的案例 2图所示。由于节点只有一个子节点,因此它可以是左子节点,也可以是右子节点。因此,该条件检查单个子节点是否为节点的左子节点。如果是这样,我们需要根据节点本身与其父节点的位置,将左子节点指向节点的父节点“左”或“右”引用。对右侧节点应用相同的规则。这里,右节点引用设置为其父节点的左或右子节点,而不是基于节点位置的引用。
由于我们已经更新了节点类,我们需要对 BST 类进行一些更改,以便插入和删除节点。插入代码如下所示:
function insert(int $data)
{
if ($this->isEmpty()) {
$node = new Node($data);
$this->root = $node;
return $node;
}
$node = $this->root;
while ($node) {
if ($data > $node->data) {
if ($node->right) {
$node = $node->right;
}
else {
$node->right = new Node($data, $node);
$node = $node->right;
break;
}
}
elseif ($data < $node->data) {
if ($node->left) {
$node = $node->left;
}
else {
$node->left = new Node($data, $node);
$node = $node->left;
break;
}
}
else {
break;
}
}
return $node;
}
代码看起来与我们之前使用的代码相似,只是有一个小改动。现在,我们在创建新节点时发送当前节点引用。此当前节点将用作新节点的父节点。new Node($data, $node)代码实际上起到了作用。
要删除节点,我们可以先进行搜索,然后使用 node 类中的delete方法删除搜索到的节点。因此,remove函数本身将非常小,就像这里的代码一样:
public function remove(int $data) {
$node = $this->search($data);
if ($node) $node->delete();
}
正如代码所示,我们首先搜索数据。如果节点存在,我们将使用delete方法删除它。现在,让我们使用remove调用运行前面的示例,看看它是否有效:
$tree->remove(15);
$tree->traverse($tree->root);
我们只是从我们的树上移除15,然后从树的根部穿过。现在我们将看到以下输出:
3
6
8
10
12
13
36
我们可以看到,15 不再是我们 BST 的一部分。通过这种方式,我们可以删除任何节点,如果我们使用相同的方法进行遍历,我们将看到一个排序列表。如果我们查看前面的输出,我们可以看到输出是按升序显示的。这背后有一个原因,我们将在下一个主题中探讨不同的树遍历方式。
You can find a great tool for visualized binary search tree operations at http://btv.melezinek.cz/binary-search-tree.html. It is a good starting for learners to understand the different operations visually.
树遍历是指我们访问给定树中每个节点的方式。根据我们如何进行遍历,我们可以遵循三种不同的遍历方式。这些遍历在许多不同的方面都非常重要。表达式求值的波兰符号转换是使用树遍历的最流行示例之一。
按顺序,树遍历首先访问左节点,然后访问根节点,然后访问右节点。对于每个节点,这将递归地继续。与根节点值相比,左节点存储的值较小,右节点存储的值大于根节点。因此,当我们应用顺序遍历时,我们将获得一个排序列表。这就是为什么到目前为止,我们的二叉树遍历显示了一个排序的数字列表。该遍历部分实际上是顺序树遍历的示例。顺序树遍历遵循以下原则:
-
通过递归调用 in order 函数遍历左子树。
-
显示根(或当前节点)的数据部分。
-
通过递归调用 in order 函数遍历右子树。

前面的树将显示 A、B、C、D、E、F、G、H 和 I 作为输出,因为它是按顺序遍历的。
在预顺序遍历中,首先访问根节点,然后是左节点,然后是右节点。预序遍历的原则如下:
- 显示根(或当前节点)的数据部分。
- 通过递归调用 pre-order 函数遍历左子树。
- 通过递归调用 pre-order 函数遍历右子树。

前面的树将以 F、B、A、D、C、E、G、I 和 H 作为输出,因为它是按预先顺序遍历的。
在后序遍历中,最后访问根节点。首先访问左节点,然后访问右节点。后序遍历的原则如下:
- 通过递归调用 post order 函数遍历左子树。
- 通过递归调用 post order 函数遍历右子树。
- 显示根(或当前节点)的数据部分。
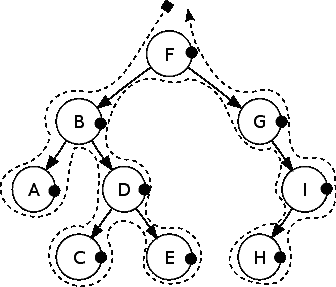
前面的树将具有输出 A、C、E、D、B、H、I、G 和 F,因为它是以后序方式遍历的。
现在,让我们在 BST 类中实现遍历逻辑:
public function traverse(Node $node, string $type="in-order") {
switch($type) {
case "in-order":
$this->inOrder($node);
break;
case "pre-order":
$this->preOrder($node);
break;
case "post-order":
$this->postOrder($node);
break;
}
}
public function preOrder(Node $node) {
if ($node) {
echo $node->data . " ";
if ($node->left) $this->traverse($node->left);
if ($node->right) $this->traverse($node->right);
}
}
public function inOrder(Node $node) {
if ($node) {
if ($node->left) $this->traverse($node->left);
echo $node->data . " ";
if ($node->right) $this->traverse($node->right);
}
}
public function postOrder(Node $node) {
if ($node) {
if ($node->left) $this->traverse($node->left);
if ($node->right) $this->traverse($node->right);
echo $node->data . " ";
}
}
现在,如果我们为前面的二进制搜索树运行三种不同的遍历方法,下面是运行遍历部分的代码:
$tree->traverse($tree->root, 'pre-order');
echo "\n";
$tree->traverse($tree->root, 'in-order');
echo "\n";
$tree->traverse($tree->root, 'post-order');
这将在命令行中生成以下输出:
10 3 6 8 12 13 15 36
3 6 8 10 12 13 15 36
3 6 8 12 13 15 36 10
到目前为止,我们已经看到了不同的树类型及其操作。不可能逐一介绍每种树类型及其不同的操作,因为这超出了本书的范围。我们希望对其他树结构及其操作复杂性有一个最低限度的了解。这是一个图表,其中包含不同类型树的不同操作和空间的平均和最坏情况复杂性。我们可能需要根据需求选择不同的树结构:
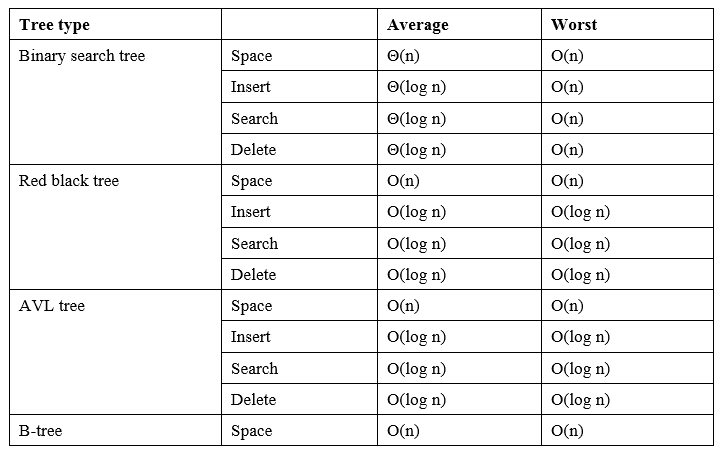
在本章中,我们详细讨论了非线性数据结构。您了解到树是分层数据结构,有不同的树类型、操作和复杂性。我们还了解了如何定义二叉搜索树。这对于实现不同的搜索技术和数据存储非常有用。在下一章中,我们将把重点从数据结构转移到算法上。我们将重点讨论第一类算法——排序算法。
 PDF电子书集合
PDF电子书集合