- 数组与链表
- 堆栈和队列
- 搜索算法
- 排序算法
- 图形结构
- 树结构
- 递归教程
关注我们

堆是平衡二叉树数据结构的一种特殊情况,其中根节点key与其子节点进行比较并进行相应安排。如果α具有子节点β,则-
key(α)≥key(β)
当父级的值大于子级的值时,此属性会生成最大堆。基于此标准,堆可以为两种类型-
For Input → 35 33 42 10 14 19 27 44 26 31
Min-Heap(最小堆) - 根节点的值小于或等于其子节点之一。
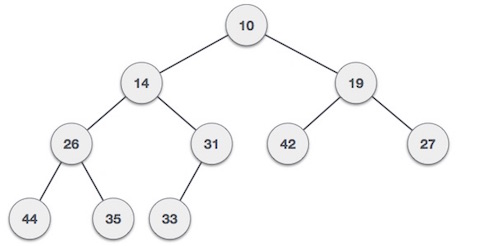
Max-Heap(最大堆) - 根节点的值大于或等于其子节点之一。
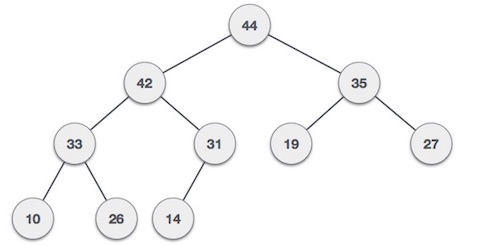
两种树都是使用相同的输入和到达顺序构造的。
最大堆构造算法
我们将使用相同的示例来演示如何创建最大堆,创建最小堆的进程类似,但是我们使用最小值而不是最大值。
注意-在"最小堆"构造算法中,我们期望父节点的值小于子节点的值。
让我们通过动画插图了解Max Heap的构造。我们考虑与之前使用的输入样本相同的样本。

最大堆删除算法
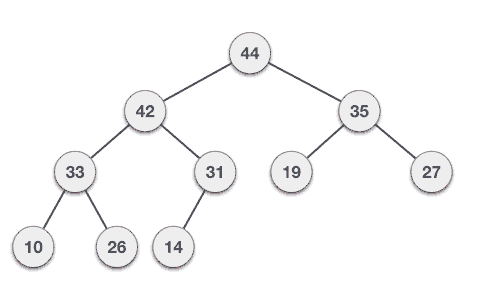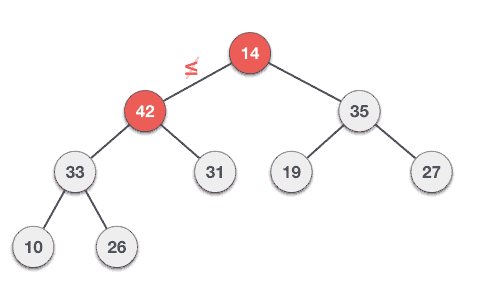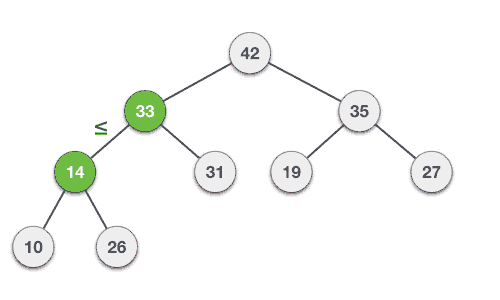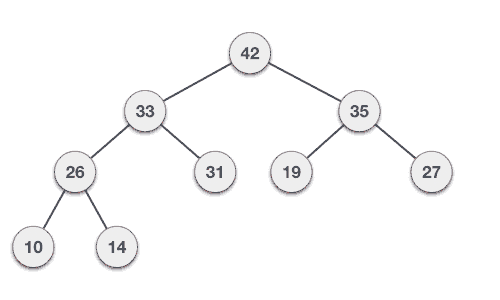
祝学习愉快!(内容编辑有误?请选中要编辑内容 -> 右键 -> 修改 -> 提交!)
好记忆不如烂笔头。留下您的足迹吧 :)
 《数据结构和算法入门教程》
《数据结构和算法入门教程》 