图解Dijkstra算法+代码实现

简介

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。 对应问题：在无向图G=(V,E)中，假设每条边E(i)的长度W(i)，求由顶点V0到各节点的最短路径。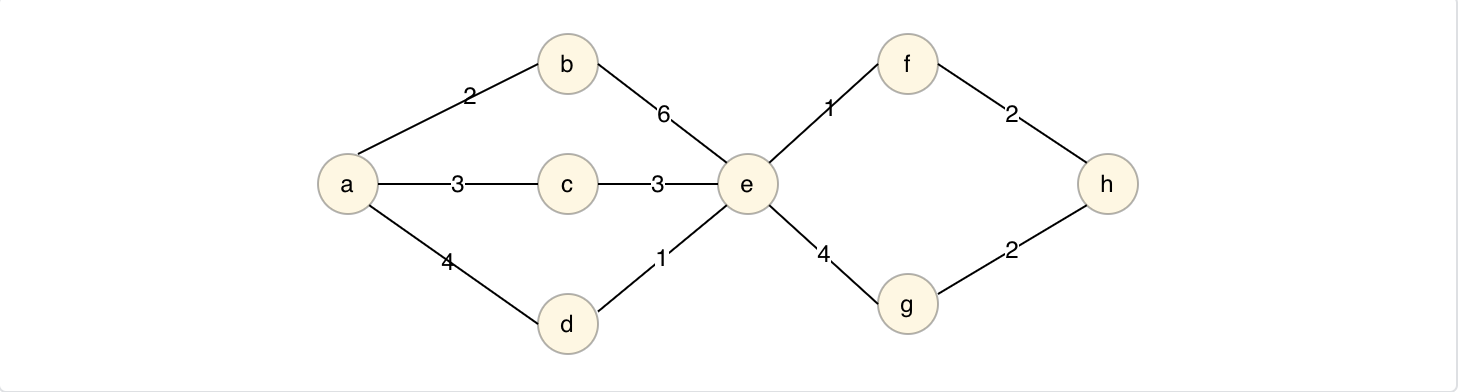

工作过程

Dijkstra算法将顶点集合分为两组，一组记录已经求得最短路径的顶点记为finallyNodes，一组正在求解中的顶点记为processNodes， step1:finallyNodes中顶点最开始只有源节点，最短路径长度为0，而processNodes中包含除源节点以外的节点，并初始化路径长度，与源节点直接相连的记路径长度为权重，不相连的记为♾️。 step2:从process中选择路径长度最小的顶点，加入finallyNodes，并且更新processNodes，将与当前顶点相连的顶点路径长度更新为min（当前权重，当前顶点最短路径长度+当前顶点与顶点相连边权重）。 step3:重复step2，直至processNodes数组为空。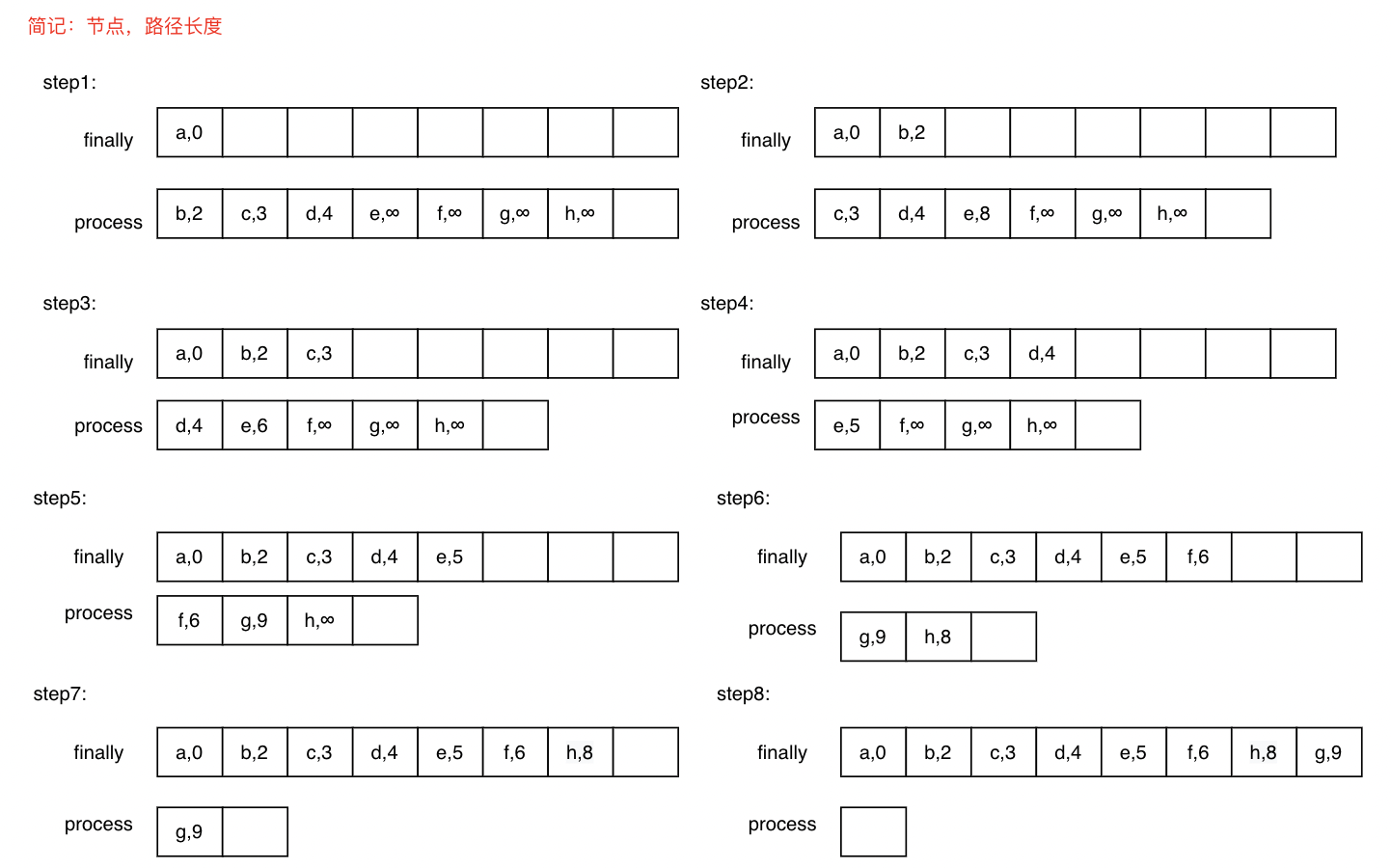

总体思路

这次我想先描述一下自己的大概思路，下面再写具体实现。 首先为了方便，我采用的是邻接表存储图结构，邻接表是一个二维数组，值存储权重。根据上面工作过程中描述的内容，我们会有两个中间集合记录，finallyNodes记录的是最终结果，我们只需要将计算的结果往里面塞即可。但是processNodes却是一个不断变化更新的集合，其中的操作包括删除节点，更改节点值，查找节点值，同时我们每次需要拿出processNodes中记录的距离最小的值，所以ProcessNodes准备用最小堆来做，那再删除节点，更改节点值之后都需要调整堆为最小堆，java自带的优先队列没有提供更改节点值的操作，因此我们这里需要自己实现一个小根堆，支持以上操作。 然后就中规中矩实现dijkstra算法即可。

实现

小根堆

如果对堆不太熟悉的可以先看看这篇文章：堆（优先队列），这里就不过多解释了，直接贴代码。 这里堆中存的数据格式为int二维数组,存储节点下标位置和对应距离，排序按存储的距离进行排序。

public class MinHeap {
        List<int[][]> heap ;
        /**
         * 获取并移除堆顶元素，并调整堆
         * @return
         */
        public int[][] pop() {
            int[][] top = heap.get(0);
            heap.set(0, heap.get(heap.size() - 1));
            heap.remove(heap.size() - 1);
            //调整堆
            this.adjust(0, heap.size() - 1);
            return top;
        }

        /**
         * 判断是否为空
         * @return true/false
         */
        public boolean isEmpty() {
            if (null == this.heap) {
                return true;
            }
            if (this.heap.size() == 0) {
                return true;
            }
            return false;
        }
        /**
         * 修改index位置节点的value值，并调整最小堆（Java priorityQueue未提供）
         * @param index 修改节点位置
         * @param value 修改值
         */
        public void changeValue(int index, int value) {
            int src = heap.get(index)[0][1];
            heap.get(index)[0][1] = value;
            //直接比较当前值是变大还是变小,然后考虑是向上调整还是向下调整
            //则当前值可能往上移动
            if (src > value) {
                this.upAdjust(index);
                return;
            }
            this.adjust(index, heap.size() - 1);
        }

        public void upAdjust(int index) {
            //依次与双亲节点进行比较，小于双亲节点就直接交换。一直到根节点
            while (index > 0) {
                int parent = index >> 1;
                //双亲节点本来小于当前节点不需要进行调整
                if (heap.get(parent)[0][1] <= heap.get(index)[0][1]) {
                    break;
                }
                swap(index, parent);
                index = parent;
            }
        }
        
        /**
         * 初始化一个最小堆
         * @param nums
         */
        public void init(int[][] nums) {
            heap = new ArrayList<>(nums.length);
            for (int i = 0 ; i < nums.length; i ++) {
                int[][] temp = new int[1][2];
                temp[0][0] = nums[i][0];
                temp[0][1] = nums[i][1];
                heap.add(temp);
            }
            //从最后一个双亲节点开始将堆进行调整
            for (int i = nums.length / 2 ; i >= 0 ; -- i) {
                this.adjust(i, nums.length - 1);
            }
        }
        /**
         * 从当前index开始调节为最小堆
         * @param index 当前节点下标
         * @param end 最后一个节点下标
         */
        private void adjust(int index, int end) {
            //找到当前节点的孩子节点，将较小的节点与当前节点交换，一直往下，直至end
            while (index <= end) {
                //左孩子节点
                int left = index << 1;
                if (left + 1 <= end && heap.get(left + 1)[0][1] < heap.get(left)[0][1] ) {
                    //找到当前较小的节点
                    ++ left;
                }
                //没有孩子节点，或者当前的孩子节点均已大于当前节点，已符合最小堆，不需要进行调整
                if (left > end || heap.get(index)[0][1] <= heap.get(left)[0][1]) {
                    break;
                }
                swap(index, left);
                index = left;
            }
        }
        private void swap(int i, int j) {
            int[][] temp = heap.get(i);
            heap.set(i, heap.get(j));
            heap.set(j, temp);
        }
    }

Dijsktra

数据结构

图节点仅存储节点值，一个Node数组nodes，存储图中所有节点，一个二维数组adjacencyMatrix，存储图中节点之间边的权重，行和列下标与nodes数组下标对应。

 //节点
 Node[] nodes;

 //邻接矩阵
 int[][] adjacencyMatrix;
public class Node {
        private char value;
        Node(char value) {
            this.value = value;
        }
    }

初始化

初始化图 values标志的图中所有节点值，edges标志图中边，数据格式为（node1的下标，node2的下标，边权重）

private void initGraph(char[] values, String[] edges) {
        nodes = new Node[values.length];
  			//初始化node节点
        for (int i = 0 ; i < values.length ; i ++) {
            nodes[i] = new Node(values[i]);
        }
        adjacencyMatrix = new int[values.length][values.length];
  			//初始化邻接表，同一个节点权重记为0，不相邻节点权重记为Integer.MAX_VALUE
        for (int i = 0 ; i < values.length ; i++) {
            for (int j = 0 ; j < values.length ; j ++) {
                if (i == j) {
                    adjacencyMatrix[i][j] = 0;
                    continue;
                }
                adjacencyMatrix[i][j] = Integer.MAX_VALUE;
                adjacencyMatrix[j][i] = Integer.MAX_VALUE;
            }
        }
  			//根据edges更新相邻节点权重值
        for (String edge : edges) {
            String[] node = edge.split(",");
            int i = Integer.valueOf(node[0]);
            int j = Integer.valueOf(node[1]);
            int weight = Integer.valueOf(node[2]);
            adjacencyMatrix[i][j] = weight;
            adjacencyMatrix[j][i] = weight;
        }
        visited = new boolean[nodes.length];

    }

初始化dijsktra算法必要的finallyNodes和processNodes

    
		/**
		* 标志对应下标节点是否已经处理，避免二次处理
		*/
		boolean[] visited;
    /**
     * 记录已经求得的最短路径 finallyNodes[0][0]记录node下标，finallyNodes[0][1]记录最短路径长度
     */
    List<int[][]> finallyNodes;
    /**
     * 记录求解过程目前的路径长度，因为每次取当前已知最短，所以最小堆进行记录
     * 但是java优先队列没有实现改变值，这里需要自己实现
     * 首先每次取出堆顶元素之后，堆顶元素加入finallyNodes，此时需要更新与当前元素相邻节点的路径长度
     * 然后重新调整小根堆
     * 首先：只会更新变小的数据，所以从变小元素开始往上进行调整，或者直接调用调整方法，从堆顶往下进行调整
     */
    MinHeap processNodes;
	/**
     * 初始化，主要初始化finallyNodes和processNodes，finallyNodes加入源节点，processNodes加入其他节点
     * @param nodeIndex
     */
    private void initDijkstra(int nodeIndex) {
        finallyNodes = new ArrayList<>(nodes.length);
        processNodes = new MinHeap();
        int[][] node = new int[1][2];
        node[0][0] = nodeIndex;
        node[0][1] = adjacencyMatrix[nodeIndex][nodeIndex];
        finallyNodes.add(node);
        visited[nodeIndex] = true;
        int[][] process = new int[nodes.length - 1][2];
        int j = 0;
        for (int i = 0 ; i < nodes.length ; i++) {
            if (i == nodeIndex) {
                continue;
            }
            process[j][0] = i;
            process[j][1] = adjacencyMatrix[nodeIndex][i];
            ++ j;
        }
        //初始化最小堆
        processNodes.init(process);
    }

dijsktra算法实现

public void dijkstra() {
        //1。堆顶取出最小元素，加入finallyNodes
  			//2。将与堆顶元素相连节点距离更新，
        while (!processNodes.isEmpty()) {
            int[][] head = processNodes.pop();
            finallyNodes.add(head);
            int nodeIndex = head[0][0];
            visited[nodeIndex] = true;
            //跟堆顶元素相邻的元素
            for (int j = 0 ; j < nodes.length ; j ++) {
                //找到相邻节点
                if (visited[j] || Integer.MAX_VALUE == adjacencyMatrix[nodeIndex][j]) {
                    continue;
                }
                for (int i = 0 ; i < processNodes.heap.size() ; i++) {
                    int[][] node = processNodes.heap.get(i);
                    //找到节点并且值变小，需要调整
                    if (node[0][0] == j && node[0][1] > head[0][1] + adjacencyMatrix[nodeIndex][j]) {
                        processNodes.changeValue(i, head[0][1] + adjacencyMatrix[nodeIndex][j]);
                        break;
                    }
                }
            }

        } 
    }

测试

public static void main(String[] args) {
        char[] values = new char[]{'A','B','C','D','E','F','G','H'};
        String[] edges = new String[]{"0,1,2","0,2,3","0,3,4","1,4,6","2,4,3","3,4,1","4,5,1","4,6,4","5,7,2","6,7,2"};
        Dijkstra dijkstra = new Dijkstra();
        dijkstra.initGraph(values, edges);
        int startNodeIndex = 0;
        dijkstra.initDijkstra(startNodeIndex);
        dijkstra.dijkstra();
        for (int[][] node : dijkstra.finallyNodes) {
            System.out.println(dijkstra.nodes[node[0][0]].value + "距离" + dijkstra.nodes[startNodeIndex].value + "最短路径为：" + node[0][1]);
        }
    }